Max Ficco about now weblog notes photos projects contact

Data Structures (CSE 20312)
Prof. Jay Brockman, Fall 2025

mooc.fi

2025-08-27

talked about unit tests and makefiles
in makefile:

The C Language!

Memory Management

sizeof(...) tells you how many bytes a datatype stores:

bool, char -- 1
short -- 2
int, float -- 4
double -- 8
int* , char* -- 8

2025-08-29

binary and hexadecimal numbers:

0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
A 1010
B 1011
C 1100
D 1101
E 1110
F 1111

At each memory address you can only store one byte

Ex:
char c = 'A'; int x = 0xaabbccdd (0x denotes hexadecimal)

name address value
c ~ 0x41
(higher address) 0xaa
~ 0xbb
~ 0xcc
x (lower address) 0xdd

pointer variables

int x = 1;
int *p; initializes start of 8 consecutive bytes in memory
p = &x sets p to x's address found in lookup table
*p = 5 changes the value at the address stored in p to 5
^ dereference * here is an operator, different than the one used to initialize pointer p

example in zybooks

#include <stdio.h>

int main()
{
    int x = 5;                  // x, y are ints
    int y = 1;
    int *p;                     // p, q are addresses of ints
    int *q;

    p = &x;                     // p gets address of x
    y = *p;                     // y gets value at address in p
    printf("y = %d\n", y);

    q = p;                      // q gets same address as p

    printf("*p = %d    *q = %d\n", *p, *q); 
}

^ used debugger to watch values change step by step

Arrays are contiguous blocks of memory
int a; a <---value of a
int A[5]; A <---points to the starting value (A[0]) of the array

char char_v1;
int  int_v1;
char char_v2;
int  int_v2;
char char_array[4];
int  int_array[4];

Address of char_v1:        0x7ffcd1389526
Address of int_v1:         0x7ffcd1389528
Address of char_v2:        0x7ffcd1389527
Address of int_v2:         0x7ffcd138952c
Address of char_array[0]:  0x7ffcd1389544
Address of char_array[1]:  0x7ffcd1389545
Address of int_array[0]:   0x7ffcd1389530
Address of int_array[1]:   0x7ffcd1389534

^ variables of same data type follow each other sequentially in memory
(i.e. by data type - not by order of declaration)

2025-09-01

pointer arithmetic

recap: arrays are contiguous blocks of memory

what happens when you add 1 to a pointer?

pointers and strings

char s[] = "abcde";
// _________________________________________________
// |  'a'  |  'b'  |  'c'  |  'd'  |  'e'  |   0   |
// | &s[0] | &s[1] | &s[2] | &s[3] | &s[4] | &s[5] |
// -------------------------------------------------

cool trick we can do:

// Keep going while *(s + i) != 0 (false). (we could have also used s[i])
for (int i = 0;  *(s + i);  i++) {
    printf("%c", *(s + i));
}

subtracting pointers

let char *p point to the '\0' in string s.
what is p-s?

memory management

Variables: have names (created by compiler)
Dynamic memory: doesn't have name, but has pointer to reach it (created at runtime)

Regions of Memory:

ffffffffffffffff
_________________
Stack (grows downward)
- contains function local variables
______ vv _______


______ ^^ _______
Heap (grows upward)
- from malloc, calloc, free
_________________               ^^ created at runtime (above)^^   vv (below) created at compile time vv
DATA FIXED SIZE
- contains global variables, static variables, constant strings
_________________
(Text) Code
- contains machine code to run program
_________________
0000000000000000

Heap: dynamic memory allocation in C

void *malloc(n_bytes)

void *calloc(n_objects, bytes_per_object)

free(void *ptr)

What happens when you call a function?

void f3() { 
	// does something
}
void f1() { 
	// does something
}
void f2() {
    f3();
}

void main() {
    f1();
    f2();
}

________  (TOP OF STACK)
| main |
-------- <-- stack pointer (points to the address below the top of the stack that has enough space for `main`'s variables)

________  (TOP OF STACK)
| main |
--------
|  f1  |
-------- <-- stack pointer 

________  (TOP OF STACK)
| main |
--------
|  f2  |
-------- <-- stack pointer 

________  (TOP OF STACK)
| main |
--------
|  f2  |
--------
|  f3  |
-------- <-- stack pointer 

________  (TOP OF STACK)
| main |
-------- <-- stack pointer

"Isn't this exceedingly clever?"
Key part of computer system design: you don't want to waste memory!
The nature of functions calling functions automatically takes care of this for you with a stack

2025-09-03

call stack example

int add(int m, int n) {
    m = m + n;
    return m;
}
void square(int *a) {
    *a = *a * *a;
}
int main() {
    int x = 1;
    int y = 1;

    int z = add(x, y);
    square(&z);

    printf("x=%d y=%d z=%d\n", x, y, z);

    return 0;
}
name address value
y 0x7...7e4 (highest in stack) 1
x 0x7...7e0 1
z 0x7...7dc 2, then 4
m 0x7...7bc 1
n 0x7...7b8 1
a 0x7...7b8 (replaces n) 0x7...7dc

Data segment

--> has global variables, statics, and string constants

char a[] = "cat"; sizeof(a): 4
on main's stack frame:

_________________________________
|  'c'  |  'a'  |  't'  |   0   |
---------------------------------

char *p = "dog"; sizeof(p): 8
"dog" is a string constant!
on main's stack frame:

_______________________________________________
|  pointer p to data segment(8 bytes)         |
-----------------------------------------------

in data segment:

_________________________________
|  'd'  |  'o'  |  'g'  |   0   |
---------------------------------

We cannot do: p[0] = 'X'! It is a string constant that lives in the data segment.
note that global variables and static variables live in the data segment and can be written to

We can however reassign p to a different address: p = &a

But we cannot make an array point to a new address: a = p is illegal.

2025-09-05

where do variables go in memory?

double GLOBAL = 3.14;
int main() {
    int int_scalar = 25;
    int int_array[] = {100, 101, 102, 103};
    char *str_const = "hello";
    int *malloc_array = malloc(10*sizeof(int))
    static int static_int = 2;

---------------------------stack----------------------------
    int_array: 0x7ffc090b24d0,    *int_array: 100
&malloc_array: 0x7ffc090b24c8,  malloc_array: 0x652de1f3d2a0
   &str_const: 0x7ffc090b24c0,     str_const: 0x652dbe49b008
  &int_scalar: 0x7ffc090b24bc,    int_scalar: 25
----------------------------heap----------------------------
 malloc_array: 0x652de1f3d2a0, *malloc_array: 0
----------------------------data----------------------------
  &static_int: 0x652dbe49d018,    static_int: 2
      &GLOBAL: 0x652dbe49d010,        GLOBAL: 3.140000
    str_const: 0x652dbe49b008,    *str_const: h
----------------------------code----------------------------
         main: 0x652dbe49a1a9,    *(unsigned char*)main: 0xf3   <- first opcode! (first byte of first instruction of main)

I/O: printing strings:

char *string = "hello"

printf("%s\n", string);

puts(string); // only takes in strings; prints with a new line

reading input line by line

can use scanf, but we'll usually use fgets

char buffer[BUFSIZ]; // BUFSIZ is a constant defined in <stdio.h> (a couple thousand characters, more than enough)
while (fgets(buffer, BUFSIZ, stdin)) {
    // process the buffer (maybe strdup into an array of strings)
}

small downside: fgets also captures newline \n. We can "chomp":

Arrays of strings

_____
| * |  strarray (on stack)
-----
  | (points to first pointer in heap) 
  |
__V__
| * | - - >|'c'|'a'|'t'|'\0'|  (each string also exists somewhere in heap, not necessarily in order among each other)
-----
| * | - - >|'d'|'o'|'g'|'\0'|
-----
| * | - - >|'m'|'o'|'u'|'s'|'e'|'\0'|
-----

To free this whole array of strings is sorta complicated:

2025-09-08

reading user data into an array of strings (continuing from last class)

char  **read_user_data(FILE *stream, int nstrings) {
    char buffer[80]; // Up to 80 characters per string
    char **sarray = calloc(nstrings, sizeof(char*)); // use calloc so that we have 0s at end to use as sentinel
    int i = 0;
    while (fgets(buffer, 80, stream)) {
        chomp(buffer);
        *(sarray+i) = strdup(buffer);
        i++;
    }
    return sarray;
}

freeing a list of strings char** strarray

using free:

  1. delete each string
  2. delete each pointer
void free_string_array(char **sarray) {
    for (int i = 0; sarray[i]; i++) {
        free(sarray[i]); // free each individual string
    }
    free(sarray); // free the array of string pointers
}

Abstract Data Types (ADTs)

Today: Dynamic Array
Wednesday: Other ADTs on top of Dynamic Array (Stack, Queue, Set)

review of structs:

Example: Point with x and y

struct Point {
    int x;
    int y;
};

nicer to do:

typdef struct {
    int x;
    int y;
} Point;

Point p; p.x = 1; p.y = 2;

Label Address Value
(y) Ox...F 0x00
(y) Ox...E 0x00
(y) Ox...D 0x00
start of y Ox...C 0x10 (2)
(x) Ox...B 0x00
(x) 0x...A 0x00
(x) 0x...9 0x00
p -> start of x 0x...8 0x01 (1) 
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef struct {
    char *name;
    int  age;
} Person;

int main() {
    // Declare a Person as a local variable
    Person p;
    p.name = "James";
    p.age = 20;

    // Allocate a Person on the heap
    Person *p_ptr = malloc(sizeof(Person));
    p_ptr->name = strdup("Madison");
    p_ptr->age = 21;

    printf("sizeof(p): %lu\n", sizeof(p)); // 16 (would have expected it to be 12 for char* and int)
    printf("sizeof(*p_ptr): %lu\n", sizeof(*p_ptr)); // 16

    free(p_ptr->name);
    free(p_ptr);
}

Dynamic Array: Overview

____________
| data     | ------> |__1__|__4__|__3__|_____|_____|
------------
| capacity | = 5 (how much total space in internal data array) 
------------
| size     | = 3 (number of elements stored within capacity)
------------

methods:

array_create()

Growing an Array: realloc

void* realloc(void *p, size_t size) (size_t typically unsigned long int)

Shifting elements to the right

                              |--[size]
                              v
|__31__|__32__|__33__|__35__|____|____|____|____|
                     ^__want to insert(34, at index 3)

from: size
to: index
we set: data[i] = data[i-1]

Computational Complexity

space/time efficiency
Big O Notation
O(1): constant
O(N): proportional to N
O(N^2): proportional to N^2
...(covered more later)

Average (A) and Worst Case (W)

Function Time (A) Time (W) Space (A) Space (W)
Append O(1) O(N) (realloc+copy) O(1) O(N)
At O(1) O(1) O(1) O(1)
Index O(N) O(N) O(1) O(1)
Insert O(N) O(N) O(1) O(N) (realloc)

2025-09-10

Dynamic Array C code

array.h

#pragma once // (so that everything is included only once)

#include <stdbool.h>
#include <stdlib.h>

/* Constants */
#define ARRAY_DEFAULT_CAPACITY 1 << 2 // 4 elements

/* Structure */
typedef struct {
    int	  *data;	// Internal array
    int   capacity;	// Total number of elements
    int   size;     // Number of valid elements
} Array;

/* Functions */
Array*  array_create();
void    array_delete(Array *array);
void    array_append(Array *array, int value);
int     array_at(Array *array, int index);
int	    array_index(Array *array, int value);
void    array_insert(Array *array, int index, int value);

array.c

#include "array.h"
#include <assert.h>
#include <string.h>

Array *array_create() {
    // Allocate Array structure
    Array *array = malloc(sizeof(Array));

    // Initialize capacity and size
    array->capacity = ARRAY_DEFAULT_CAPACITY;
    array->size = 0;

    // Allocate the data array
    array->data = malloc(array->capacity * sizeof(int));

    // return pointer to Array
    return array;
}

void array_delete(Array *array) {
    // Free the data array
    free(array->data);
    
    // Free the Array structure
    free(array);
}

void array_append(Array *array, int value) {
    // If the size is at capacity, double the capacity
    if (array->size == array->capacity) {
        array->capacity *= 2;
        array->data = realloc(array->data, array->capacity * sizeof(int));
    }
    // Store value at end of array and increment size
    array->data[array->size] = value;
    array->size++;
}

int array_at(Array *array, int index) {
    // Return the value at the index
    return array->data[index];
}

int array_index(Array *array, int value) {
    // Scan internal array for first element 
    // that matches value and return its index         
    for (int index = 0; index < array->size; index++)
        if (array->data[index] == value) {
            return index;
        }
    return -1; // Return -1 if no match found
}

void array_insert(Array *array, int index, int value) {
    // If the size is at capacity, double the capacity
    if (array->size == array->capacity) {
        array->capacity *= 2;  // Double the capacity
        array->data = realloc(array->data, array->capacity * sizeof(int));
    }

    // Shift the values from index to the end of the array one element ahead
    for (int i=array->size; i>index; i--) {
        array->data[i] = array->data[i-1];
    }

    // Store new value and increment size
    array->data[index] = value;
    array->size++;
}

Stack: Overview

Push: add element to top
Pop: remove element from top
Top: peek at top
Empty: true if stack is empty

|   | 
|   |
| 3 | <--Top of Stack
| 2 |
| 1 | 
-----

Parentheses, Brackets, Braces Matching:

valid PBB Matching:

(){}[]
{[()]}
{}[]

invalid:

[)]
[{()]}

We can use the stack to write an algorithm to detect valid PBBs!:
traverse string in order left to right:

for each input char c:
	if c is an opener:
		push c on stack
	else:
		if stack empty: return false
		if c is closer that matches top:
			pop stack
		else:
			return false
if stack is empty:
	return true
else:
	return false

2025-09-12

Implementing Stack, based on our previous implementation of Dynamic Array

stack.h

#pragma once
#include "array.h"

/* Structures */
typedef Array Stack;

/* Functions */
Stack*  stack_create();
void    stack_delete(Stack *stack);
void    stack_push(Stack *s, int value);
int     stack_pop(Stack *s);
int     stack_top(Stack *s);
bool    stack_empty(Stack *s);

stack.c

#include "stack.h"
#include <assert.h>

Stack* stack_create() {
    return array_create();
}

void stack_delete(Stack *stack) {
    array_delete(stack);
}

void stack_push(Stack *stack, int value) {
    array_append(stack, value);
}

int stack_top(Stack *stack) {
    assert(stack->size > 0);
    return array_at(stack, stack->size - 1);
}

int stack_pop(Stack *stack) {
    int top = stack_top(stack); // will assert false if stack is empty
    stack->size--;
    return top;
}

bool stack_empty(Stack *stack) {
    return stack->size == 0;
}

Implementing Parentheses, Brackets, Braces Matching Algorithm:

#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#include "stack.h"

void chomp(char *str) {
    size_t size = strlen(str);
    if (*(str + size - 1) == '\n') *(str + size - 1) = 0;
}

bool is_pbb_matched(char *s) {
    Stack *stack = stack_create();

    for (char *c = s; *c; c++) {
        // if char is an opener, push 
        if (*c == '{' || *c == '[' || *c == '(') {
            stack_push(stack, *c); // push ascii value of opener
        // else if char is a closer that match opener on stack, pop
        } else if (!stack_empty(stack) && 
                    ((*c == '}' && stack_top(stack) == '{') ||
                    (*c == ']' && stack_top(stack) == '[') ||
                    (*c == ')' && stack_top(stack) == '('))) {
            stack_pop(stack);
        // else no match
        } else {
            stack_delete(stack);
            return false;
        }
    }
    if (stack_empty(stack)) {
        stack_delete(stack);
        return true;
    } else {
        stack_delete(stack);
        return false;
    }
}

int main(int argc, char *argv[]) {
    char buffer[BUFSIZ];
    while (fgets(buffer, BUFSIZ, stdin)) {
        chomp(buffer);
        puts(is_pbb_matched(buffer) ? "pbb-matched" : "not pbb-matched");
    }
    return 0;
}

Stack vs. Queue

stack: Last In, First Out (LIFO)

___________________v---push and pop only on one end
|
--------------------

queue: First In, First Out (FIFO)

pop---v___________________v---push
         (like a pipe!)
       -------------------

methods for queue:

Complexity of Queue (implemented with a Dynamic Array):

Function Time (Avg) Space (Avg)
Push O(1) O(1)
Pop O(N) - have to shift everything O(1)
Front O(1) O(1)
Empty O(1) O(1)

deque (double ended queue):

push, pop--v_________________________________v---push, pop
             (pipe that can flow either way) 
            ---------------------------------

methods for queue:

Set

Complexity of Set (implemented with a Dynamic Array):

Function Time (Avg) Space (Avg)
Add O(1) O(1)
Contains O(N) O(1)
Remove O(N) O(1)

Algorithm analysis

constant time operations: operations that take the same amount of time regardless of data value

Big O Notation:

Classic Big O Complexities:

O(1)

O(N)

O(N^2), and other polynomials

O(log N)

|__0__|__3__|__7__|__9__|__25__|__47__|__83__|
					 ^--look at mid: > or < than key? (discard other half & repeat until mid==key)

O(N log N)

O(C^N), O(N!) - exponential, non-polynomial

2025-09-15

Comparing linear and binary search times

binary search is much faster!!
10,000 trials on sorted array of 2^(20) elements:

Some examples: what is their complexity?

example 1: dot products
O(N) because each element is multiplied and added pairwise

example 2: matrix multiplication
O(N^3)

for each row
	for each column
		take dot product - O(N)

example 3:
Euclidian GCD - greatest common divisor of a and b
(where N is bit length of a and b)

  1. Ensure that a is greater than b. If b is greater than a, swap the values of a and b.
  2. Computer the remainder of r of a divided by b
  3. If r is equal to 0, then the GCD of a and b is b. Otherwise, set a to b and b to r, and go back to step 2

Recursion

Why recursion?

Basic recursive function:

recursive(data):
	if (base case):
		perform base action
		return
	else
		recursive(reduced data)

Variants:

Examples:

int cumulative_sum(int n) {
    if (n == 0) {
        return 0;
    }
    return n + cumulative_sum(n-1);
}

int factorial(int n) {
    if (n == 0) {
        return 1;
    }
    return n * factorial(n - 1);
}

void print_string(char *s) { // "every string is a character followed by another string"
    if (*s == '\0') {
        putchar('\n');
        return;
    }
    putchar(*s);
    print_string(s+1);
}

2025-09-17

continuing recursion:

void reverse_array(int *list, int start_index, int end_index) {
    if (start_index >= end_index) { // 0 or 1 elements left in middle
        return;
    }
    // swap elements
    int temp = list[start_index];
    list[start_index] = list[end_index];
    list[end_index] = temp;

    reverse_array(list, start_index + 1, end_index - 1);
}

int linear_search(int *numbers, int high, int key) {
    if (high < 0) {
        return -1;
    }
	if (numbers[high] == key) {
        return high;
    }

    return linear_search(numbers, high - 1, key);
}

int binary_search(int *numbers, int low, int high, int key) {
	if (low > high)
		return -1;

	int mid = (low + high) / 2;

	if (key > numbers[mid])
		return binary_search(numbers, mid+1, high, key);

	if (key < numbers[mid])
		return binary_search(numbers, low, mid-1, key);

   return mid;
}

bool has_duplicate(int *array, int high) {
    if (high == 0)
        return false;

    if (linear_search(array, high-1, array[high]) >= 0)
        return true;

    return has_duplicate(array, high-1);
}

int fibonacci_number(int n) {
	if (n == 0)
		return 0;
	if (n == 1)
		return 1;
	return fibonacci_number(n - 1) + fibonacci_number(n - 2);
}

Recurrence Relations

Recurrence relation for factorial:

(k)
 |
(k)
 |
(k)
 |
... (repeated n times)

T(N) = k + T(N-1) => O(N)

Recurrence relation for has_duplicate:

(N)
 |
(N-1)
 |
(N-2)
 |
... (repeated n times)

T(N) = N + T(N-1)
	 = N + N-1 + ... + 1 = (N+1)*(N/2) => O(N^2)

Sorting

Sorting Cards Exercise

2025-09-19

Bubble Sort

void BubbleSort(int *numbers, int numbersSize) {
   for (int i = 0; i < numbersSize - 1; i++) {
      for (int j = 0; j < numbersSize - i - 1; j++) {
         if (numbers[j] > numbers[j+1]) {
            int temp = numbers[j];
            numbers[j] = numbers[j + 1];
            numbers[j + 1] = temp;
         }
      }
   }
}
// or...
void BubbleSort(int *numbers, int numbersSize) {
   int i = numbersSize - 1;
   while (i > 0) {
      for (int j = 0; j < i; j++) {
         if (numbers[j] > numbers[j + 1]) {
            int temp = numbers[j];
            numbers[j] = numbers[j + 1];
            numbers[j + 1] = temp;
         }
      }
      i--;
   }
}

Insertion Sort

void InsertionSort(int *numbers, int numbersSize) {
    for (int i = 1; i < numbersSize; ++i) {
        int j = i;
            // Insert numbers[i] into sorted part
            // stopping once numbers[i] in correct position
            while (j > 0 && numbers[j] < numbers[j - 1]) {
            // Swap numbers[j] and numbers[j - 1]
            int temp = numbers[j]; 
            numbers[j] = numbers[j - 1];
            numbers[j - 1] = temp;
            --j;
        }
    }
}

Space Complexity

Adaptiveness and Stability

Adaptiveness: Takes advantage of partial sort

void BubbleSortImproved(int *numbers, int numbersSize) {
   int last;  // last swap index
   for (int i = 0; i < numbersSize - 1; /* i updated below using last */) {
      last = -1;
      for (int j = 0; j < numbersSize - i - 1; j++) {
         if (numbers[j] > numbers[j + 1]) {
            int temp = numbers[j];
            numbers[j] = numbers[j + 1];
            numbers[j + 1] = temp;
            last = j;
         }
      }
      if (last == -1) break;                 // already sorted
      i = numbersSize - last - 1;            // shrink checked range
   }
}
// or...
void BubbleSortImproved(int *numbers, int numbersSize) {
   int i = numbersSize - 1;
   while (i >= 1) {
      int last = -1;
      for (int j = 0;  j < i;  j++) {
         if (numbers[j] > numbers[j+1]) {
            int temp = numbers[j];
            numbers[j] = numbers[j + 1];
            numbers[j + 1] = temp;
            last = j;
         }
      }
      i = last;
   }
}

We can also improve insertion sort (saves on write instructions):

void InsertionSortImproved(int *numbers, int numbersSize) {
    for (int i = 1;  i < numbersSize;  i++) {
        int j = i - 1;
        int tmp = numbers[i];
        while ((j >= 0) && (numbers[j] > tmp)) {
            numbers[j+1] = numbers[j];
            j = j - 1;
        }
        numbers[j+1] = tmp;
    }
}

Stability: If two elements have the same the value, order will not be changed

O(N^2) sorting algorithms build up sorted region through multiple passes

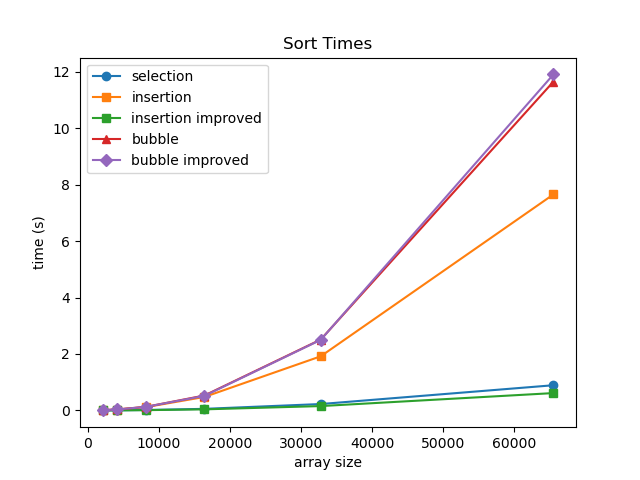
o-n-squared-sorting-times

O(N log N) sorting algorithms build up a sorted order by dividing the problem and combining results.

Merge sort

did example in class physically sorting 16 people by first name using merge sort (cool!)

  • start as individual
  • merge into pairs
  • merge pairs into new order (only comparing first of each pair)
  • pair groups of 4 ... and so on ...(only comparing first of each order)

best, average, and worst time complexity: O(N log N)
space complexity: O(N) - need ancillary array of size N

Quicksort

average time complexity: O(N log N) - usually, depending on data/choices
average space complexity: O(log N) - auxiliary due to recursion stack

pivot_value = 4 (pick middle element)

|__3__|__6__|__1__|__4__|__7__|__2__|__5__|
   ^--low_index                        ^--high_index

while low_index <= high index:
	increment low_index until array[low_index] > pivot_value
	decrement high_index until array[high_index] < pivot_value
	swap array[low_index] with array[high_index]

then, given ending position of low_index,
	recursively apply sort on low partition (orig_low_index to ending_low_index) 
	recursively apply sort on high partition (ending_low_index+1 to orig_high_index)

Worst case: if pivots are always bad, it basically turns into selection sort

2025-09-22

Merge Sort Visualization
Quicksort & Merge Sort

Recap:

Merge Sort C code

#include <stdlib.h>

void Merge(int *numbers, int i, int j, int k) {
   int mergedSize = k - i + 1;               // Size of merged partition
   int mergePos = 0;                         // Position to insert merged number
   int leftPos = 0;                          // Position of elements in left partition
   int rightPos = 0;                         // Position of elements in right partition
   // Dynamically allocates temporary array for merged numbers
   int *mergedNumbers = malloc(mergedSize * sizeof(int));   
   leftPos = i;                          // Initialize left partition position
   rightPos = j + 1;                     // Initialize right partition position
   
   // Add smallest element from left or right partition to merged numbers
   while (leftPos <= j && rightPos <= k) {
      if (numbers[leftPos] <= numbers[rightPos]) {
         mergedNumbers[mergePos] = numbers[leftPos];
         ++leftPos;
      }
      else {
         mergedNumbers[mergePos] = numbers[rightPos];
         ++rightPos;
         
      }
      ++mergePos;
   }
   
   // If left partition is not empty, add remaining elements to merged numbers
   while (leftPos <= j) {
      mergedNumbers[mergePos] = numbers[leftPos];
      ++leftPos;
      ++mergePos;
   }
   
   // If right partition is not empty, add remaining elements to merged numbers
   while (rightPos <= k) {
      mergedNumbers[mergePos] = numbers[rightPos];
      ++rightPos;
      ++mergePos;
   }
   
   // Copy merge number back to numbers
   for (mergePos = 0; mergePos < mergedSize; ++mergePos) {
      numbers[i + mergePos] = mergedNumbers[mergePos];
   }
   free(mergedNumbers);
}

void MergeSort(int *numbers, int i, int k) {
   int j = 0;
   
   if (i < k) {
      j = (i + k) / 2;  // Find the midpoint in the partition
      
      // Recursively sort left and right partitions
      MergeSort(numbers, i, j);
      MergeSort(numbers, j + 1, k);
      
      // Merge left and right partition in sorted order
      Merge(numbers, i, j, k);
   }
}
MERGE SORT Time Complexity Space Complexity
Best Case O(N log N) O(N)
Average Case O(N log N) O(N)
Worst Case O(N log N) O(N)
--
Adaptive? No
Stable? Yes

side note: python uses Timsort, which essentially uses merge sort down to subarrays of 32 elements, and then uses insertion sort (which is adaptive)

Quicksort

#include <stdbool.h>

int Partition(int *numbers, int lowIndex, int highIndex) {
    // Pick middle element as pivot
    int midpoint = lowIndex + (highIndex - lowIndex) / 2;// avoids overflow, otherwise same as (highIndex + lowIndex) / 2;
    int pivot = numbers[midpoint];

    bool done = false;
    while (!done) {
        while (numbers[lowIndex] < pivot) {
            lowIndex += 1;
        }
        while (pivot < numbers[highIndex]) {
            highIndex -= 1;
        }
        // If zero or one elements remain, then all numbers are partitioned. Return highIndex.
        if (lowIndex >= highIndex) {
            done = true;
        } else {
            // Swap numbers[lowIndex] and numbers[highIndex]
            int temp = numbers[lowIndex];
            numbers[lowIndex] = numbers[highIndex];
            numbers[highIndex] = temp;
            // Update lowIndex and highIndex
            lowIndex += 1;
            highIndex -= 1;
        }
    }
    // this will be the top of the low end for the next call
    return highIndex;
}

void Quicksort(int *numbers, int lowIndex, int highIndex) {
    // Base case: If the partition size is 1 or zero
    // elements, then the partition is already sorted
    if (lowIndex >= highIndex) {
        return;
    }
    // Partition the data within the array. Value lowEndIndex
    // returned from partitioning is the index of the low
    // partition's last element.
    int lowEndIndex = Partition(numbers, lowIndex, highIndex);
	
    Quicksort(numbers, lowIndex, lowEndIndex);// recursively sort low partition
    Quicksort(numbers, lowEndIndex + 1, highIndex);// recursively sort high partition
}

// from https://anim.ide.sk/sorting_algorithms_2.php
// Basically the same thing, may do one extra swap with itself
void Quicksort(int *a, int beg, int end) {
	int i = beg;
    int j = end;
    int pivot = a[(i + j) / 2];
	while (i <= j) {  // i, j need to cross for next call
		while (a[i] < pivot) 
            i++;
        while (a[j] > pivot) 
            j--;
        if (i <= j) {
            // one last swap with yourself--no harm
            int temp = a[i];
            a[i] = a[j];
            a[j] = temp;
            i++;
            j--;
        }
    }
    if (beg < j) 
        Quicksort(a, beg, j);
    if (i < end) 
        Quicksort(a, i, end);
}
QUICKSORT Time Complexity Space Complexity
Best Case O(N log N) O(log N)
Average Case O(N log N) O(log N)
Worst Case O(N^2) O(N)
--
Adaptive? No
Stable? No

Comparison:

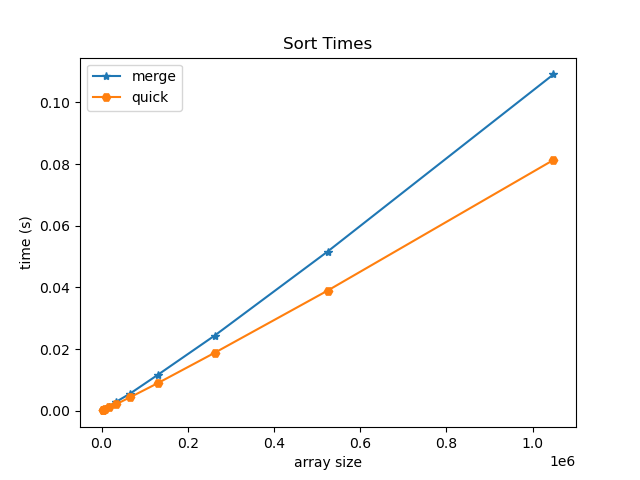
mergesort_quicksort
NOTE: we did not cover radix sort in class, but may it be useful to review for interviews!

2 main data structure implementations:

  1. (dynamic) array based
  2. linked

Linked Data structures:

For Recursive Data Structures:

Linked Lists

made up of list nodes:

		_________      _________
Value:	| Blue  |      |  Red  |
		---------      ---------
Next:	|   *---|-->   |   *---|--> null
		---------      ---------
*Head-------^

first element in list we call the head

in class balloon demo: when inserting/removing elements, don't let go of any balloons! (memory leaks/dangling pointers)

insert node at head of list

Node *list_add_head(Node *head, int value) {
    Node *n = malloc(sizeof(Node));
    n->value = value;
    n->next = head;
    return n;
}

delete node from head of list

Node *list_remove_head(Node *head) {
    Node *n = head;
    head = n->next;
    free(n);
    return head;
}

2025-09-24

...continuing Linked Lists:
recap: when allocating variables on the heap, unless you maintain contact with them (using pointer), the balloon will float away (memory leak)!

Pointer Chasing (printing a linked list)

head --> [ ] --> [ ] --> [ ] --> 0
set n = head, move down the list!

void list_print_iterative(Node *head) {
    for (Node *n = head; n != NULL; n = n->next) { // don't do n++! nodes are not sequential like arrays
        printf("%d ", n->value);
    }
    printf("\n");
}

Adding node after current node

         curr
	      ↓
head --> [1] -x-> [3] --> [4] --> 0
	      ↓        ↑
 (malloc) n  -->  [2]

void list_add_after(Node *curr, int value) {
    Node *n = malloc(sizeof(Node));
    n->value = value;
    n->next = curr->next;
    curr->next = n;
}

Removing node after current node

         curr            successor
	      ↓     (free!)    ↓ 
head --> [1] -x-> [3] --> [4] --> 0
	      ↓                ↑
          -->-->-->-->-->--^

void list_remove_after(Node *curr) {
    Node *successor = curr->next->next;
    free(curr->next);
    curr->next = successor;
}

Print list recursively

void list_print_recursive(Node *head) {
    if (head == NULL) {
        printf("\n");
        return;
    }
    printf("%d ", head->value);
    list_print_recursive(head->next);
}

void list_print_reversed_recursive(Node *head, Node *curr) {
    if (curr == NULL) {
        return;
    }
    list_print_reversed_recursive(head, curr->next); // recurse _before_ we print
    printf("%d ", curr->value);
    if (curr == head) printf("\n"); // same head is passed to every recursive call
}
// called as: list_print_reversed_recursive(head, head);

Deleting a Linked LIst

void list_delete_iterative(Node *head) {
    while (head != NULL) {
        Node *n = head;
        head = head->next;
        free(n);
    }
}
void list_delete_recursive(Node *head) {
    if (head == NULL) {
        return;
    }
    list_delete_recursive(head->next); // recurse first!
    free(head);
}

Stack implemented using Linked List

recall:

for linked lists:

Queue using a Linked List

								  tail (push only)
								  ↓
head --> [ ] --> [ ] --> [ ] --> [ ] --> 0

2025-09-26

Queue using Linked list

recap:

Deque (double ended queue) using Doubly-Linked List

				 (head)                         (tail)
				_________      _________      _________
Value:			| Blue  |      |  Red  |      | Green |
				---------      ---------      ---------
Next:			|   *---|-->   |   *---|-->   |   *---|--> null
				---------      ---------      ---------
Prev:   null <--|---*   |   <--|---*   |   <--|---*   |
				---------      ---------      ---------

  head                                   tail
   ↓                                      ↓ 
[dummy] <-> [10] <-> [20] <-> [30] <-> [dummy]

Doubly Linked List Implementation

#include <stdio.h>
#include <stdlib.h>

// Definition of a Node
typedef struct Node {
    int data;
    struct Node* prev;
    struct Node* next;
} Node;

// Definition of a Doubly Linked List
typedef struct DoublyLinkedList {
    Node* head;  // Dummy head
    Node* tail;  // Dummy tail
} DoublyLinkedList;

// Create a new node
Node* create_node(int data) {
    Node* new_node = (Node*)malloc(sizeof(Node));
    new_node->data = data;
    new_node->prev = new_node->next = NULL;
    return new_node;
}

// Initialize the doubly linked list with Dummy nodes
DoublyLinkedList* create_list() {
    DoublyLinkedList* list = (DoublyLinkedList*)malloc(sizeof(DoublyLinkedList));
    list->head = create_node(0);  // Dummy head
    list->tail = create_node(0);  // Dummy tail
    list->head->next = list->tail;
    list->tail->prev = list->head;
    return list;
}

// Check if the list is empty
int is_empty(DoublyLinkedList* list) {
    return list->head->next == list->tail;
}

// Helper function: Insert node after current node
void insert_after(Node *current, int data) {
    Node* new_node = create_node(data);
    Node* next_node = current->next;

    current->next = new_node;
    new_node->prev = current;
    new_node->next = next_node;
    next_node->prev = new_node;
}

// Helper function: Remove current node and return data
int pop(Node* current) {
    int data = current->data;
    current->prev->next = current->next;
    current->next->prev = current->prev;
    free(current);
    return data;
}

// Prepend an element to the head  of the list
void prepend(DoublyLinkedList* list, int data) {
    insert_after(list->head, data);
}

// Append an element to the tail of the list
void append(DoublyLinkedList* list, int data) {
    insert_after(list->tail->prev, data);
}

// Remove the (non-dummy) head of the list and return value
int pop_head(DoublyLinkedList* list) {
    return pop(list->head->next);
}

// Remove the (non-dummy) head of the list and return value
int pop_tail(DoublyLinkedList* list) {
    return pop(list->tail->prev);
}

// Insert an element at a specific position (0-based index)
void insert_at(DoublyLinkedList* list, int data, int position) {
    Node* current = list->head;
    int i = 0;

    // Traverse the list to find the position
    while (current->next != list->tail && i < position) {
        current = current->next;
        i++;
    }

    insert_after(current, data);
}

// Delete an element at a specific position (0-based index)
void delete_at(DoublyLinkedList* list, int position) {
    Node* current = list->head->next;  // Start from the first valid node
    int i = 0;

    // Traverse to the node at the specified position
    while (current != list->tail && i < position) {
        current = current->next;
        i++;
    }

    // If we are at a valid node (not the Dummy tail)
    if (current != list->tail) {
        pop(current);
    }
}

// Delete an element by value
int delete_by_value(DoublyLinkedList* list, int data) {
    Node* current = list->head->next;  // Start from the first valid node
    while (current != list->tail) {
        if (current->data == data) {
            pop(current);
            return 1;  // Data found and deleted
        }
        current = current->next;
    }
    return 0;  // Data not found
}

// Display the list forward
void display_forward(DoublyLinkedList* list) {
    printf("Head <-> ");
    Node* current = list->head->next;  // Start from the first valid node
    while (current != list->tail) {
        printf("%d <-> ", current->data);
        current = current->next;
    }
    printf("Tail\n");
}

// Display the list backward
void display_backward(DoublyLinkedList* list) {
    printf("Tail <-> ");
    Node* current = list->tail->prev;  // Start from the last valid node
    while (current != list->head) {
        printf("%d <-> ", current->data);
        current = current->prev;
    }
    printf("Head\n");
}

// Free the memory allocated for the list
void free_list(DoublyLinkedList* list) {
    Node* current = list->head;
    while (current != NULL) {
        Node* next = current->next;
        free(current);
        current = next;
    }
    free(list);
}

Note: we can actually implement doubly linked list with a single dummy node (this is how python implements deque)

2025-09-29

recap: doubly linked lists - dummy nodes aren't necessary but are helpful for avoiding extra checks

Employee Record Database

Employee Record object (struct)

Operations:

if implemented using dynamic array, lookup is O(N) if unsorted, else O(log N)

what if we use the employee id as the index?

[name][name][name][name] ... [name]
   0     1     2     3         9999

Now, lookup is O(1), but we need to use a massive array!

solution: use "buckets" instead of single name string per index

|__| |__| |__| |__|  ... |__|
|__| |__| |__| |__|  ... |__|
|__| |__| |__| |__|  ... |__|
  0    1    2    3         999
^ instead of indexing by id, index by last 3 elements of id!

Now, suppose we wanted to lookup people by name to get id?

A good hash function:
- Doesn't reduce info much
- ex: not ideal to reduce 26^5 possible 5 letter words into 130 buckets
- Maintains randomness

Load factor of a hash table

Def: number of records (size) / the capacity (# of buckets)
ex:

     |__|
null |__| |__| null
  0    1    2    3

load factor = 3/4 = 0.75

Alpha (α): when load factor is greater than α, triggers resizing & rehashing of hash table

Pair Structure

typedef struct {
    char *key;
	int value;
    Pair *next;
} Pair;

Table Structure

typedef struct {
    Pair **buckets;
    int capacity;
    int size;
} Table;

Pair functions

#include "pair.h"
#include <stdlib.h>
#include <string.h>

Pair *pair_create(const char *key, int value, Pair *next) {
    Pair *p = calloc(1, sizeof(Pair));
    p->key = strdup(key);
    p->value = value;
    p->next = next;
    return p;
}

void pair_delete(Pair *p) {
    if (!p) return;

    pair_delete(p->next);
    free(p->key);
    free(p);
}

Basic Hash Function (sum of ascii values)

int	hash(char *str) {    
    int value = 0;
    for (int i = 0; str[i] != '\0'; i++) {
    	value += str[i];
    }
    return value;
}

Table functions

#include "table.h"
#include "hash.h"
#include <stdio.h>
#include <string.h>

Table *table_create() {
    Table *t = calloc(1, sizeof(Table));
    t->capacity = TABLE_DEFAULT_CAPACITY;
    t->buckets = calloc(t->capacity, sizeof(Pair *));
    return t;
}

void table_delete(Table *t) {
    for (int bucket = 0; bucket < t->capacity; bucket++) {
        pair_delete(t->buckets[bucket]);
    }

    free(t->buckets);
    free(t);
}

int table_lookup(Table *t, char *key) {
    int bucket = hash(key) % t->capacity;
    
    // look for the key in the bucket's chain of pairs and return value if you find it.
    for (Pair *p = t->buckets[bucket]; p != NULL; p = p->next) {
        if (strcmp(p->key, key) == 0) {
            return p->value;
        }
    }
    return -1; // key is not found
}

void table_insert(Table *t, char *key, int value) {
    if (table_lookup(t, key) != -1) {
        return;
    }
    // inserts a pair at the head of the bucket's chain
    int bucket = hash(key) % t->capacity;
    t->buckets[bucket] = pair_create(key, value, t->buckets[bucket]);

    t->size++;
}

void table_print(Table *t) {
    for (int bucket = 0; bucket < t->capacity; bucket++) {
        printf("Bucket %d: ", bucket);
        for (Pair *curr = t->buckets[bucket]; curr; curr = curr->next)
            printf(" {%s: %d}", curr->key, curr->value);
        printf("\n");
    }
}

2025-10-01

what if we don't want to use linked lists in each bucket?

Linear Probing

Hash table: Want to insert 11, 19, 30, 15, 22
|___|___|___|___|___|___|___|___|
  0   1   2   3   4   5   6   7

|_22|___|___|_11|_19|___|_30|_15|
  0   1   2   3   4   5   6   7
                  ^--bucket 3 was already full
  ^--buckets 6&7 were full (loops around)

Collisions and Hashing

Hash table: Want to insert 2, 10, 18
|___|___|_*_|___|___|___|___|___|
  0   1   2   3   4   5   6   7

what number abdefg do we choose?

Fast Hashing: Shift and add

String hash

djb2 - Daniel J. Bernstein

unsigned long hash(unsigned char *str) {
	unsigned long hash = 5381;
	int c;
	while (c = *str++)
		hash = ((hash << 5) + hash) + c; // hash = hash * 33 + c
	return hash;
}

Comparing hash functions

table index: 4 bits
table size:  16 buckets
all keys collide on bin: 1
 key  key^2       binary key^2  mid-square  knuth
   1      1                  1       0         9
  17    289          100100001       8         8
  33   1089        10001000001       8         6
  49   2401       100101100001       6         4
  65   4225      1000010000001       8         2
  81   6561      1100110100001      10         0
  97   9409     10010011000001       6        15
 113  12769     11000111100001      15        13
 129  16641    100000100000001       8        11

Note:

How many buckets?

2025-10-03

Moving from C to Python

Recall: C dynamic Array

typedef struct {
    int	  *data;	// Internal array
    int   capacity;	// Total number of elements
    int   size;     // Number of valid elements
} Array;

/* Functions */
Array*  array_create();
void    array_delete(Array *array);
void    array_append(Array *array, int value);
int     array_at(Array *array, int index);
int	    array_index(Array *array, int value);
void    array_insert(Array *array, int index, int value);

C++ implementation (object-oriented extension from C):

class Array {
private:
	int *data
	int capacity
	int size
public:
	Array(); // constructor
	~Array(); // destructor
	
	void append(int value);
	int at(int index) const;
	int index_of(int value) const;
	void insert(int index, int value);
	int get_size() const;
}

int main() {
	Array arr;
	arr.append(10);
	arr.append(20);
	arr.insert(1, 15);
	
	std::cout << "arr[1] is " << arr.at(1) << std::endl;
	std::cout << "Value 20 is at index " << arr.index_of(20) << std::endl;

	return 0;
}

Abstraction

Def: hiding private implementation details and exposing a public interface through methods

Inheritance

Def: Child class takes methods and attributes from parent

Polymorphism

Def: type-specific methods with the same name

Python built-in types

<class 'int'> <class 'float'> <class 'str'> <class 'list'> <class 'set'> <class 'dict'> <class 'tuple'>

Magic methods

Listing of methods for Python base object (from which all objects inherit!):
['__class__', '__delattr__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__']

Looking at CPython!

List implementation:
listobject.c

Set implementation:
setobject.c

From listsort.txt:

Intro
-----
This describes an adaptive, stable, natural mergesort, modestly called
timsort (hey, I earned it <wink>).  It has supernatural performance on many
kinds of partially ordered arrays (less than lg(N!) comparisons needed, and
as few as N-1), yet as fast as Python's previous highly tuned samplesort
hybrid on random arrays.

In a nutshell, the main routine marches over the array once, left to right,
alternately identifying the next run, then merging it into the previous
runs "intelligently".  Everything else is complication for speed, and some
hard-won measure of memory efficiency.

Some recommended resources:
w3schools.com
tutorialspoint.com
realpython.com
docs.python.org

2025-10-06

Review for Midterm Exam

Know your powers of 2!

2^0 = 1
2^1 = 2
2^2 = 4
2^3 = 8
2^4 = 16
2^5 = 32
2^6 = 64
2^7 = 128
2^8 = 256
2^9 = 512
2^10 = 1024 (roughly 10^3)
...
2^20 = 1,048,576 (roughly 10^6)
2^30 = 1,073,741,824 (roughly 10^9)
2^40 = 1,099,511,627,776 (roughly 10^12)

Every 10 powers of 2 is roughly 3 powers of 10

To find other powers, use nearest multiple of 10:
2^15 = (2^10)(2^5) = roughly 32000 (actually 32768)
2^23 = (2^20)(2^3) = roughly 8 million (actually 8388608)
2^25 = (2^20)(2^5) = roughly 32 million (actually 33554432)
2^32 = (2^30)(2^2) = roughly 4 billion (actually 4294967296)

Storage Reference:

Recall: Regions of Memory

int p = 3

int main() {
	int i = 25;
	char a[] = "wx";
	char *s = "yz";
	int *m = malloc(10 * sizeof(int));
	static int t = 2;
	
	*m = 100;
	*(m + 1) = 101;
	m[2] = 103;
}

Assume 6-bit memory address: 0x00 - 0x3F (0-63)
Assume each memory location has enough bits to hold an int, char, or address

STACK HEAP DATA CODE
3F: i: 25 2F: 1F: 0F:
3E: '\0' 2E: 1E: 0E:
3D: 'x' 2D: 1D: 0D:
3C: a: 'w' 2C: 1C: 0C:
3B: s: 0x11 2B: 1B: 0B:
3A: m: 0x20 2A: 1A: 0A:
39: 29: 19: 09:
38: 28: 18: 08:
37: 27: 17: 07:
36: 26: 16: 06:
35: 25: 15: 05:
34: 24: 14: t: 2 04:
33: 23: 13: '\0' 03:
32: 22: 103 12: 'z' 02:
31: 21: 101 11: 'y' 01:
30: 20: 100 10: p: 3 00: main: *m = 100

remember, in reality, usually:

in-class activity: Kahoot!

2025-10-08

Midterm Exam

2025-10-10

Running Python in VSCode

python3 first_script.py

if python file contains #!/usr/bin/env python3 at the top:
chmod +x first_script.py
./first_script.py

Use the VS Code debugger

  1. Set a breakpoint in your program
  2. Click the debugger icon in the sidebar
  3. Click Run and Debug (no need for a launch.json file)
  4. Select Python Debugger (only need to set this the first time)
  5. Select Python File Debug the currently active Python file as the configuration (only need to set this the first time)

Tip: If you want to set a breakpoint where there isn't conveniently a line to stop on, such as at the very end of a script, you can add a pass statement.

basic python stuff

# Adding two numbers
x = 5
y = 10
z = x + y
print(z)

# Adding two strings
x = "Hello"
y = "World"
z = x + " " + y
print(z)

# Formatting strings (f-strings)
x = 75
y = 25
z = f"The sum of {x} and {y} is {x + y}"
print(z)

# While loop and if statement
x = 0
while x < 5:
    if x % 2 == 0:
        print(x)
    x += 1

# For loop
# Note: range(5) only goes up to 4
for x in range(5):
    if x % 2 == 0:
        print(x)

# list
x = [100, 200, 300, 400, 500]
x.append(600)
x[2] = 350

# for loop with list
for y in x:
    print(y)

# slicing a list
# Note: x[1:3] only includes elements at index 1 and 2
y = x[1:3]
print(y)

y = x.pop(0)
print(y)

# dictionary
x = {"a": 100, "b": 200, "c": 300}
x["d"] = 400
x["a"] = 150
if ("a" in x):
    print("Key 'a' exists")

# set
x = set()
x.add(100)
x.add(200)
x.add(300)
x.remove(200)
print(x)

Unit Testing

# functions.py
def add(a, b): return a + b
def subtract(a, b): return a - b
def multiply(a, b): return a * b
def divide(a, b): return a / b

# call_functions.py
import functions

def main():
    print(functions.add(5, 3))
    print(functions.subtract(5, 3))
    print(functions.multiply(5, 3))
    print(functions.divide(5, 3))

if __name__ == "__main__":
    main()

# functions_test.py
import functions
import unittest

class TestFunctions(unittest.TestCase):
    def test_add(self):
        self.assertEqual(functions.add(5, 3), 8)

    def test_subtract(self):
        self.assertEqual(functions.subtract(5, 3), 2)

    def test_multiply(self):
        self.assertEqual(functions.multiply(5, 3), 15)

    def test_divide(self):
        self.assertEqual(functions.divide(12, 3), 4)

if __name__ == "__main__":
    unittest.main() # runs all the methods with wrappers around them for debugging purposes

Equality & Identity

Boolean & Comparison

Membership & Sequence

Type & Instance

Exceptions & Warnings

with self.assertRaises(ValueError):
    divide(10, 0)

Use the VS Code Testing panel

  1. VS Code has been configured to automatically recognize any file of the form test.py as containing unittest objects
  2. Click on the flask icon in the VS Code sidebar to open the Testing panel
  3. Click on the play icon next to a unit test to run it, or else click on a play button higher up in the expansion to run them all.
  4. Break a unit test, test again, set breakpoint, and click on the Debug Test icon next to the test in the sidebar

VSCode is cool!

2025-10-13

Today's topics:

remember, we use dummy elements for convenience (not performance)

  head                                   tail
   ↓                                      ↓ 
[dummy] <-> [10] <-> [20] <-> [30] <-> [dummy]

Parsing data from stdin

import sys

def main():
    # Read input from stdin and chomp the newline at the end
    input = sys.stdin.read().strip()

    # Split the input into a list of strings
    number_str_list = input.split()

    # Convert the list of strings into a list of integers
    # Note: This is a list comprehension (more compact alternative to for loop)
    numbers = [int(num) for num in number_str_list] # could even add an if clause at the end!

    # Increment each number by 1
    incremented_numbers = [num + 1 for num in numbers]

    # Convert the list of integers into a list of strings
    incremented_numbers_str_list = [str(num) for num in incremented_numbers]

    # Join the list of strings into a single string with commas and spaces
    print(', '.join(incremented_numbers_str_list))

if __name__ == "__main__":
    main()

Node Class and Constructor Method

class Node:
	def __init__(self, data):
		self.data = data
		self.next = None # equivalent to NULL pointer
		self.next = None

# To instantiate:
some_node = Node(7) # self is a hidden parameter that is sent to Node.__init__

Private and Public Methods

Class DoublyLinkedList

Constructor:
	DoublyLinkedList()
Private:
	_insert_after(node, data)
	_pop_node(node)
Public:
	append(data)
	insert(index, data)
	pop(index)
	clear()
	index(data)
Magic Methods:
	supports print:
		__str()__
	supports emptiness check:
		__bool()__
	suports `in`:
		__contains(data)__
	supports for ... in:
		__iter()__
		__next()__

doubly_linked_list.py

class Node:
    # Constructor for a node with data
    def __init__(self, data):
        self.data = data
        self.next = None
        self.prev = None

class DoublyLinkedList:
    # Constructor for an empty list
    def __init__(self):
        self.head = Node(None)
        self.tail = Node(None)
        self.head.next = self.tail
        self.tail.prev = self.head
        # Used for __iter__ which supports the syntax: `for data in dll:`
        self.iter_state = None # this is the current node that we point to while traversing
    
    # Insert a new node after the given node
    # This is a private method and should not be called directly from outside the class
    def _insert_after(self, node, data):
        new_node = Node(data)
        new_node.next = node.next
        new_node.prev = node
        node.next.prev = new_node
        node.next = new_node
    
    # Remove the given node and return its data
    # This is a private method and should not be called directly from outside the class
    def _pop_node(self, node):
        node.prev.next = node.next
        node.next.prev = node.prev # note how we don't do any freeing! (automatic garbage collection)
        return node.data
    
    # Insert after the last node
    def append(self, data):
        self._insert_after(self.tail.prev, data)
  
    # Insert before the node at the given index
    def insert(self, index, data):
        node = self.head
        for _ in range(index):
            if node == self.tail:
                raise IndexError
            node = node.next
        self._insert_after(node, data)

    # Remove and return the data of the node at the given index
    def pop(self, index):
        node = self.head.next
        for _ in range(index):
            if node == self.tail:
                raise IndexError
            node = node.next
        return self._pop_node(node)  

    # Remove all nodes except head and tail
    def clear(self):
        self.head.next = self.tail
        self.tail.prev = self.head
    
    # Return the index of the first node with the given data
    def index(self, data):
        index = 0
        node = self.head.next
        while node != self.tail:
            if node.data == data:
                return index
            index += 1
            node = node.next
        return -1

    # Return a string representation of the list - supports `str(dll)`
    def __str__(self):
        return " ".join([str(d) for d in self])

    # Return True if the list is not empty
    # Supports the `if dll:` syntax to check if the list is not empty
    def __bool__(self):
        return self.head.next != self.tail
    
    # Return True if the list contains a node with the given data (supports the syntax: data in dll)
    def __contains__(self, data):
        node = self.head.next
        while node != self.tail:
            if node.data == data:
                return True
            node = node.next
        return False

    # Initialize the iterator state (return self)
    def __iter__(self):
        self.iter_state = self.head.next # (our starting value)
        return self
    
    # Return the next data from the iterator and increment iterator
    def __next__(self):
        if self.iter_state == self.tail:
            raise StopIteration
        data = self.iter_state.data
        self.iter_state = self.iter_state.next
        return data

demo

import doubly_linked_list as dll

lst = dll.DoublyLinkedList() # Create a doubly linked list

lst.append(1) # Append some data
lst.append(2)
lst.append(3)

lst.insert(1, 10) # Insert some data

d = lst.pop(1) # Pop some data

i = lst.index(3) # Find the index of some data

s = str(lst) # Get the string representation of the list
print(lst)

if lst: # Test if the list is empty
    print("List is not empty")

if 3 in lst: # Test if the list contains some data
    print("List contains 3")
if not 4 in lst:
    print("List does not contain 4")

for data in lst: # Iterate over the list
    print(data)

lst.clear() # Clear the list

if not lst: # Test if the list is empty
    print("List is empty")

2025-10-15

Introduction to Binary Trees

        8         <- root node (the one node with no parent; "top" node)
      /   \
     3     10     <- internal nodes (a node with at least one child; includes root)
    / \      \
   1   6      14  <- (14 is a child of 10, and a parent of 13)
  / \         /
 4   7      13    <- leaf nodes (a node with no children)

    [root]
     /  \
 [left] [right]

Applications of trees: anything that has a hierarchical structure

Perfect Binary Tree

       O
     /   \
    O     O
   / \   / \
  O   O O   O

Full Binary Tree

               O
           /       \
         O           O
       /   \       /   \
      O     O     O     O
     / \         / \  
    O   O       O   O

(this tree is full but neither complete nor perfect)

Complete Binary Tree

               O
           /       \
         O           O
       /   \       /   \
      O     O     O     O
     / \   /
    O   O O

(this tree is complete but neither full nor perfect)

Binary Search Tree (BST)

	2
   / \
  1   3
or...
    3
   /
  2
 /
1
or...
1
 \
  2
   \
    3

This is a BST:

    30
  /    \
 10     50
  \    /  \
  20  40  70
         /
       60

This is not a BST: (60 > 50)

    30
  /    \
 10     50
  \    /  \
  20  40  70
        \ 
        60

BST Search (Recursive)

search(tree, value) -> T/F (where tree is a pointer to the root)

Base Case:
	Node is NULL/None -> return False
Base Case:
	Node.value matches value -> return True
Recursive Case:
	if value > Node.value -> return search(Node.right) 
	else -> return(Node.left)

BST search runtime

2025-10-17

Implementing Binary Trees in Python

BST Insert (recursive)

insert(root, key)
	if root is None
		return new node with key
		
	if key == root.key
		// do nothing (we only store unique values)
	if key < root.key
		root.left = insert(root.left, key)
	if key > root.key
		root.right = insert(root.right, key)
		
	return root

example from Zybooks without using recursion (much more painful):

BSTInsert(tree, node)
	if (tree->root is null)
		tree->root = node
	else
		currentNode = tree->root
		while (currentNode is not null) {
	         if (node->key < currentNode->key) {
	            if (currentNode->left is null)
	               currentNode->left = node
	               currentNode = null
	            else
	               currentNode = currentNode->left
	         }
	         else {
	            if (currentNode->right is null)
	               currentNode->right = node
	               currentNode = null
	            else
	               currentNode = currentNode->right
	         }
		}

Prefixing variable/method names in python:

Implementing a BSTree Class, starting with Search and Insert

from tree_print import pretty_tree
import sys

class Node:
    def __init__(self, key, left=None, right=None):
        self.key = key
        self.left = left
        self.right = right

class BSTree:
    # Constructor
    # Optionally, you can initialize the tree with a root node
    def __init__(self, root=None):
        self.root = root
    
    # Clear the tree
    def clear(self):
        self.root = None # automatic garbage collection!

    # Insert a Node with a given key into the tree
    def insert(self, key):
        self.root = self._insert(self.root, key)

    # Helper function for insert
    def _insert(self, root, key):
        if root is None:
            return Node(key)
            
        if key < root.key:
            root.left = self._insert(root.left, key)
        elif key > root.key:
            root.right = self._insert(root.right, key)
        # if key == root.key, nothing happens

        return root

    # Magic method: check if the tree contains a key
    # Support for the 'in' operator
    def __contains__(self, key):
        return self._search(self.root, key)
    
    # Helper function for contains
    def _search(self, root, key):
        if root is None:
            return False
        if root.key == key:
            return True
        if key < root.key:
            return self._search(root.left, key)
        return self._search(root.right, key)
	
	def __str__(self):
        return pretty_tree(self)
		
	# more next class...

(using an external library to pretty-print our trees!)

BST insert algorithm complexity

2025-10-27

Recap on Binary Search Trees:

BST Inorder Traversal

Base Case:
	if root is None, return
Recursive:
	traverse left child (left subtree)
	print root value
	traverse right child (left subtree)

what if we want to return a list? (use + to concatenate lists)

Base Case:
	if root is None, return [] (empty list)
Recursive:
	return traverse(left child) + [root value] + traverse(right child)

(or we could append to a static/global list)

What if we don't use recursion?

Returning to our code from last class...

BSTree Class: Implementing Inorder Traversal, length, and height of tree

    # Inorder traversal
    def inorder(self):
        return self._inorder(self.root)

    # Helper function for inorder
    def _inorder(self, root):
        if not root:
            return []
        return self._inorder(root.left) + [root.key] + self._inorder(root.right)

    # Magic method: et the length of the tree 
    # Support for the len() function 
    def __len__(self):
        return self._len(self.root)
    
    # Helper function for len
    def _len(self, root):
        if not root:
            return 0
        return self._len(root.left) + self._len(root.right) + 1
    
    # Get the height of the tree
    def height(self):
        return self._height(self.root)
    
    # Helper function for height
    def _height(self, root):
        if root == None:
            return -1
        left_height = self._height(root.left)
        right_height = self._height(root.right)
        return 1+max(left_height, right_height)

For the rest of class, Prof. Brockman talked about using ai tools (e.g., Gemini Code Assist) in VSCode

2025-10-29

Removing BST Nodes

what we want:
root = remove(root, key) (the root might change after removal)

Base Case:
	if root is None, return None (trivial base case)
Recursive Case:
	if key < root.key
		root.left = remove(root.left, key)
	else if key > root.key
		root.right = remove(root.right, key)
	else (the current root == key)
		Case 1: root has no children
			return None
			
		Case 2: root only has left child
			return root.left
		Case 3: root only has right child
			return root.right
			
		Case 4: root has 2 children, height == 1
			new_root = root.right
			new_root.left = root.left
			
		Case 4+: root has 2 children, height > 1
			find the smallest node in the right tree:
				- go to right subtree and keep going left
				- this node will either be a leaf node, or have one child
			store the value of the smallest node in the right subtree (the immediate successor)
			remove that smallest node in the right subtree
			reassign the root to the stored value of the immediate successor
	
	return root

continuing in BSTree from last class...

    # Remove a Node with a given key from the tree  
    def remove(self, key):
        self.root = self._remove(self.root, key)
    
    # Helper function for remove
    def _remove(self, root, key):
        if root is None:
            return root
        
        # Key is not yet found
        if key < root.key:
            root.left = self._remove(root.left, key)
        elif key > root.key:
            root.right = self._remove(root.right, key)

        # Key is found
        else:
            # Node with only one child or leaf node: return the non-null child
            # If the node has no children, return None
            if root.left is None:
                return root.right
            if root.right is None:
                return root.left
            
            # Node with two children: Get the inorder successor (smallest in the right subtree)
            root.key = self._min_value_node(root.right)
            # Delete the inorder successor
            root.right = self._remove(root.right, root.key)
        return root
    
    # Helper function to find the minimum value node in a tree
    def _min_value_node(self, root):
        current = root
        while current.left is not None:
            current = current.left
        return current.key

Time Complexity

Space Complexity

2025-10-31

Depth-First and Bread-First Search of Binary Trees


class Node:
    def __init__(self, key, left=None, right=None):
        self.key = key
        self.left = left
        self.right = right

class BinaryTree:
    # Constructor; Optionally, you can initialize the tree with a root node
    def __init__(self, root=None):
        self.root = root

    # Depth first search: preorder traversal
    def dfs(self):
	    frontier_stack = [self.root]
        visited_list = []
        while frontier_stack:
	        current = frontier_stack.pop()
            if current is not None:
                visited_list.append(current.key)
                frontier_stack.append(current.right)
                frontier_stack.append(current.left)
        return visited_list
    
    # Breadth first search: level order traversal
    def bfs(self):
        frontier_queue = [self.root]
        visited_list = []
        while frontier_queue:
            current = frontier_queue.pop(0)
            if current is not None:
                visited_list.append(current.key)
                frontier_queue.append(current.left)
                frontier_queue.append(current.right)
        return visited_list
    
if __name__ == "__main__":

    # Create a binary tree
    #     __1__
    #    /     \
    #   2       3
    #  / \     / \
    # 4   5   6   7

    root = Node(1)
    root.left =  Node(2)
    root.right = Node(3)
    root.left.left = Node(4)
    root.left.right = Node(5)
    root.right.left = Node(6)
    root.right.right = Node(7)
    bt = BinaryTree(root)

    print("Depth-first search:")
    print(bt.dfs())
    print()
    print("Breadth-first search:")
    print(bt.bfs())
    print()

Result:

Depth-first search:
[1, 2, 4, 5, 3, 6, 7]

Breadth-first search:
[1, 2, 3, 4, 5, 6, 7]

Recursive BFS and DFS

just for sake of comparison, here are the recursive implementations of Depth-First Search and Breadth-First Search

def dfs_recursive(node, visited):
    if not node:
        return
    visited.append(node.key)
    dfs_recursive(node.left, visited)
    dfs_recursive(node.right, visited)

from collections import deque
def bfs_recursive(queue, visited):
    if not queue:
        return
    next_level = deque()
    for node in queue:
        visited.append(node.key)
        if node.left: next_level.append(node.left)
        if node.right: next_level.append(node.right)
    bfs_recursive(next_level, visited)

Preorder / Inorder / Postorder

    A
   / \
  B   C
 / \
D   E

Preorder (N → L → R)

Iterative DFS with stack is nearly always preorder traversal
Inorder and postorder rely on waiting until after children are processed, which is tricky with a stack

Inorder (L → N → R)

Postorder (L → R → N)

Reminder: These apply to DFS only, not to BFS (which uses level order).

BFS is very useful with Complete Trees!

	      1
	   /     \
	  2       3
	 / \     / \
	4   N   5   N
   / \
  N   N

using BFS to print this tree gives us:
[1, 2, 3, 4, None, 5, None, None, None]
(we can then remove the trailing None values)

Finishing our BSTree Class with a BFS method!

    def write_bfs(self):
        # If the tree is empty, return an empty list
        if self.root is None:
            return []
        
        # Push the root node to the queue
        queue = [self.root]

        # List to store the BFS traversal results
        bfs = []

        # While there are nodes to process
        while queue:
            # Pop the first node from the queue
            node = queue.pop(0)

            # If the node is None (missing children), append None to the BFS list
            if node is None:
                bfs.append(None)
            
            # If the node is not None, append its key to the results and push its children to the queue
            else:
                bfs.append(node.key)
                queue.append(node.left)
                queue.append(node.right)
        
        # Remove trailing None values
        while bfs and bfs[-1] is None:
            bfs.pop()
        
        # Return the BFS traversal list
        return bfs

2025-11-3

AVL Trees

Motivation - say we insert 1, 3, 5, 9 in order:

1
 \
  3
   \
    5
     \
      9

Here, our tree is essentially just a linked list! We won't get any of the logarithmic benefits of trees!

Key Idea: Rotation

Can rotate tree around a node while maintaining BST ordering properties
starting from:

1
 \
  2
   \
    3

rotate left:

  2
 / \
1   3

starting from:

    3
   /
  2
 /
1

rotate right:

  2
 / \
1   3

General Case: Rotate Left

  4
 / \
2   6
   / \
  5   7
       \
        8

rotate left:

    6
   / \
  4   7
 / \   \
2   5   8

General Case: Rotate Right

      4
     / \
    2   6
   / \
  1   3
 /
0

rotate right:

    2
   / \
  1   4
 /   / \
0   3   6

Detecting Imbalance

Modifying our Node subclass:

Node:
- key
- left
- right
- height

Example: Height and Balance Factor

Add 47, then 21&76, then 55, then 45

	   47  h=0->1->2
	  /  \ 
h=0  21  76 h=0->1->2
         /
        55  h=0->1
       /
      45  h=0

Imbalance: 4 possible cases

"left-left":
balance factor of root > 1 (imbalance, root is left heavy)
balance factor of root.left > 0 (child is left heavy)

    3
   /
  2
 /
1

To fix: ROTATE RIGHT

"right-right":
balance factor of root < -1 (imbalance, root is right heavy)
balance factor of root.right < 0 (child is right heavy)

1
 \
  2
   \
    3

To fix: ROTATE LEFT

"left-right":
balance factor of root > 1 (imbalance, root is left heavy)
balance factor of root.left < 0 (child is right heavy)

  3 
 /
1
 \
  2

To fix:

  1. Left rotate around (1)
    • becomes a "left-left"
  2. Right rotate around root

"right-left":
balance factor of root < -1 (imbalance, root is right heavy)
balance factor of root.right > 0 (child is left heavy)

1
 \
  3
 /
2

To fix:

  1. Right rotate around (3)
    • becomes a "right-right"
  2. Left rotate around root

Balance Example 1

  40
 /  \
20   60
    /  \
   50  70 
         \
         75

unbalance around root because left height = 0, right hight = 2 (balance factor = -2)

     60
    /  \
   40  70 
  /  \   \
 20  50  75

Balance Example 2

  40
 /  \
20   60
    /  \
   50  70 
      /
	 65

	   60 
     /    \
   40      70 
  /  \    /
 20  50  65

Balance Example 3

  40
 /  \
20  60
   /  \
  50  70 
    \
    55

  40
 /  \
20  50
      \
      60
     /  \
	55  70

then we rotate left about the root:

     50
    /  \
  40   60
 /    /  \
20	 55  70

2025-11-5

Implementing AVL Tree Class in Python

from tree_print import pretty_tree

class Node:
    def __init__(self, key, left=None, right=None):
        self.key = key
        self.left = left
        self.right = right
        self.height = 0

class AVLTree:
    # Constructor
    # Optionally, you can initialize the tree with a root node
    def __init__(self, root=None):
        self.root = root
    
    # Clear the tree
    def clear(self):
        self.root = None

    # Helper function to get the height of a node for AVL balancing
    # Note: The height of a null node is -1
    def _get_height(self, node):
        if not node:
            return -1
        return node.height
    
    # Helper function to update the height of a node
    def _update_height(self, node):
        if node:
            node.height = 1 + max(self._get_height(node.left), self._get_height(node.right))
        
    
    # Helper function to get the balance factor of a node
    # Note: The balance factor of a null node is 0
    def _balance_factor(self, node):
        if not node:
            return 0
        return self._get_height(node.left) - self._get_height(node.right)

    # Helper functions to rotate left for AVL balancing
    def _rotate_left(self, z):
        """
        Example:
            Given the following tree:
            z
           / \
          T1  y
             / \
            T2  T3

            After _left_rotate(z), the tree becomes:
              y
             / \
            z   T3
           / \
          T1  T2
        """
        # Do the rotation
        y = z.right
        t2 = y.left

        y.left = z
        z.right = t2

        # Update the heights
        self._update_height(z)
        self._update_height(y)

        # Return the new root
        return y

    # Helper functions to rotate right for AVL balancing
    def _rotate_right(self, z):
        """
        Example:
            Given the following tree:
              z
             / \
            y  T3
           / \
          T1  T2

            After _right_rotate(z), the tree becomes:
              y
             / \
            T1  z
               / \
              T2  T3
        """
        # Do the rotation
        y = z.left
        T2 = y.right

        y.right = z
        z.left = T2

        # Update the heights
        self._update_height(z)
        self._update_height(y)

        # Return the new root
        return y

    def _balance(self, node):
        # update height
        self._update_height(node)

        # left heavy
        if self._balance_factor(node) > 1:
            # left child is right heavy
            if self._balance_factor(node.left) < 0:
                node.left = self._rotate_left(node.left)
            return self._rotate_right(node)

        # right heavy
        if self._balance_factor(node) < -1:
            # right child is left heavy
            if self._balance_factor(node.right) > 0:
                node.right = self._rotate_right(node.right)
            return self._rotate_left(node)

        return node

    # Insert a Node with a given key into the tree
    def insert(self, key):
        self.root = self._insert(self.root, key)

    # Helper function for insert
    def _insert(self, root, key):
        # Regular BST insertion
        if root is None:
            return Node(key)
        
        if key == root.key:
            return root
        
        if key < root.key:
            root.left = self._insert(root.left, key)
        else:
            root.right = self._insert(root.right, key)

        # return balanced tree
        return self._balance(root)
    
    # Remove a Node with a given key from the tree  
    def remove(self, key):
        self.root = self._remove(self.root, key)
    
    # Helper function for remove
    def _remove(self, root, key):
        # Regular BST removal
        if root is None:
            return root
        
        # Key is not yet found
        if key < root.key:
            root.left = self._remove(root.left, key)
        elif key > root.key:
            root.right = self._remove(root.right, key)

        # Key is found
        else:
            # Node with only one child or leaf node: return the non-null child
            # If the node has no children, return None
            if root.left is None:
                return root.right
            if root.right is None:
                return root.left
            
            # Node with two children: Get the inorder successor (smallest in the right subtree)
            root.key = self._min_value_node(root.right)
            # Delete the inorder successor
            root.right = self._remove(root.right, root.key)

        # return balanced tree
		return self._balance(root)
    
    # Helper function to find the minimum value node in a tree
    def _min_value_node(self, node):
        current = node
        while current.left is not None:
            current = current.left
        return current.key
    
    # Write the BFS traversal of the tree to a list
    def write_bfs(self):
        # If the tree is empty, return an empty list
        if self.root is None:
            return []
        
        # Push the root node to the queue
        queue = [self.root]

        # List to store the BFS traversal results
        bfs = []

        # While there are nodes to process
        while queue:
            # Pop the first node from the queue
            node = queue.pop(0)

            # If the node is None (missing children), append None to the BFS list
            if node is None:
                bfs.append(None)
            
            # If the node is not None, append its key to the results and push its children to the queue
            else:
                bfs.append(node.key)
                queue.append(node.left)
                queue.append(node.right)
        
        # Remove trailing None values
        while bfs and bfs[-1] is None:
            bfs.pop()
        
        # Return the BFS traversal list
        return bfs
    
    # Magic method: string representation of the tree
    # Support for the print() function
    def __str__(self):
        return pretty_tree(self)

2025-11-7

Note: Type hints are just "hints" and are not checked or enforced by the Python interpreter.

Python Iterables, Iterators, and Generators

Problem we're trying to solve:

Implementing With Magic Methods: Two Approaches

Example (Old Way): Linked List

head --> [ ] --> [ ] --> [ ] --> [ ] --> None
tail -----------------------------^

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class LinkedList:
    def __init__(self):
        self.head = None
        self.tail = None

    def append(self, data):
        new_node = Node(data)
        if not self.head:
            self.head = new_node
            self.tail = new_node
        else:
            self.tail.next = new_node
            self.tail = new_node

    def __str__(self):
        return self.recursive_function(self.head)
    
    # Function recursively returns a string representation of the linked list
    def recursive_function(self, current):
        if not current:
            return ''
        return str(current.data) + ' ' + self.recursive_function(current.next)

    def __iter__(self):
        # attribute added on the fly!
        self.current = self.head
        return self

    def __next__(self):
        if not self.current:
            raise StopIteration # signal to python tuntime system that you've reached the end of the list
        else:
            data = self.current.data
            self.current = self.current.next
            return data

# ---- Example usage ----
        
# Create a linked list and append some elements
lst = LinkedList()
lst.append(1)
lst.append(2)
lst.append(3)

# Print the type of the linked list
print("Print using __str__:")
print(f"type(lst.__str__()): {type(lst.__str__())}")
print(lst)

# Iterate over the linked list using a for loop
print()
print("Iterate using for loop:")
for i in lst:
    print(i)

# Iterate over the linked list using a while loop and generator
print()
print("Iterate using while loop and generator:")
iterator = iter(lst)
print(f"type(iterator): {type(iterator)}")
while True:
    try:
        print(next(iterator))
    except StopIteration:
        print("End of list")
        break

# Convert the linked list to a list
print("Convert iterable to list: list(lst)")
print(list(lst))

Why Use Generators?

def firstn(n):
    num = 0
    while num < n:
        yield num
        num += 1

Modifying the Linked List Example to Use Generator:

    def __iter__(self):
        return self.recursive_generator(self.head)
    
    # Generator function recursively yields the elements of the linked list
    def recursive_generator(self, current):
        if not current:
            return
        yield current.data
        yield from self.recursive_generator(current.next)

2025-11-10

Heap

Max Heap: Every node's key is greater than or equal to that of its children
Min Heap: Every node's key is less than or equal to that of its children

Push/Pop Time Complexity: O(logN) (only along one branch of the tree)

Example Min Heap:

     3
   /   \
  6     4
 / \    /
8   7  8

Example Max Heap:

     9
   /    \
  5      7
 / \    / \
3   4  2   2

This is not a Min Heap:

     3
   /    \
  6      4
 / \    /
8   1  8

This is not a Heap (not complete):

    O
   / \
  O   O
 / \   \
O   O   O

Heap Push

Suppose we had a heap like this:

    O
   / \
  O   O
 /
O

After pushing, we know our resulting topology will always look like this:

    O
   / \
  O   O
 / \
O   O

Then, we swap values around as needed

Example: Pushing 8

    6
   / \
  5   2
 / \   
2   8

We Bubble/Percolate the value 8 up the tree, by swapping parent and children

    8
   / \
  6   2
 / \   
2   5

Heap Pop

Example: Popping 6 (the root)

    6
   / \
  5   2
 / \   
2   3

We replace the root with the rightmost node of the last layer (last value in bfs of the complete tree; so that tree remains complete)
Then, we Bubble/Percolate Down, swapping the parent with the max child (or min child for min heap)

    5
   / \
  3   2
 /    
2

It would seem that we would need a doubly-linked tree to do bubbling, or at least some complicated recursive algorithm...but,

We don't even need a linked data structure!!

     A
   /   \
  B     C
 / \    /
D   E  F

BFS traversal gives us the array:
[a, b, c, d, e, f]

There are formulas that let us know what the parent is!

i: index of parent
2i+1: index of left-child
2i+2: index of right-child

j: index of child
(j-1)//2: index of parent

MaxHeap: Push

let's push in order: 10, 2, 5, 18, 22

start with 10:

    10

push 2:

   10
  /
 2

push 5:

   10
  /  \
 2    5

push 18:

     10
    /  \
   2    5
  /
 18

bubble it up...

     18
    /  \
   10   5
  /
 2

push 22:

     18
    /  \
   10   5
  /  \
 2    22

bubble it up...

     22
    /  \
   18   5
  /  \
 2    10

This would return the array:
[22, 18, 5, 2, 10]

continuing this example, if we pop the root:

     18
    /  \
   10   5
  /
 2

our array becomes: [18, 10, 5, 2]

Next time...Heapsort!

2025-11-12

Recall that that we represent a heap as an array, where the root is at index 0

i: index of parent
2i+1: index of left-child
2i+2: index of right-child

j: index of child
(j-1)//2: index of parent

class MaxHeap:

    def __init__(self):
        self.heap_array = []
        
    def percolate_up(self, node_index):
        while node_index > 0:
            # compute the parent node's index
            parent_index = (node_index - 1) // 2
            
            # check for a violation of the max heap property
            if self.heap_array[node_index] <= self.heap_array[parent_index]:
                # no violation, so percolate up is done.
                return
            else:
                # swap heap_array[node_index] and heap_array[parent_index]
                print("   percolate_up() swap: %d <-> %d" % (self.heap_array[parent_index], self.heap_array[node_index]))
                temp = self.heap_array[node_index]
                self.heap_array[node_index] = self.heap_array[parent_index]
                self.heap_array[parent_index] = temp
                
                # continue the loop from the parent node
                node_index = parent_index

    def percolate_down(self, node_index):
        child_index = 2 * node_index + 1
        value = self.heap_array[node_index]

        while child_index < len(self.heap_array):
            # Find the max among the node and all the node's children
            max_value = value
            max_index = -1
            i = 0
            while i < 2 and i + child_index < len(self.heap_array):
                if self.heap_array[i + child_index] > max_value:
                    max_value = self.heap_array[i + child_index]
                    max_index = i + child_index
                i = i + 1

            # check for a violation of the max heap property
            if max_value == value:
                return
            else:
                # swap heap_array[node_index] and heap_array[max_index]
                print("   percolate_down() swap: %d <-> %d" % (self.heap_array[node_index], self.heap_array[max_index]))
                temp = self.heap_array[node_index]
                self.heap_array[node_index] = self.heap_array[max_index]
                self.heap_array[max_index] = temp
                
                # continue loop from the max index node
                node_index = max_index
                child_index = 2 * node_index + 1

    def insert(self, value):
        # add the new value to the end of the array.
        print("insert(%d):" % value)
        self.heap_array.append(value)
        
        # percolate up from the last index to restore heap property.
        self.percolate_up(len(self.heap_array) - 1)
        
    def remove(self):
        # save the max value from the root of the heap.
        print("remove():")
        max_value = self.heap_array[0]
        
        # move the last item in the array into index 0.
        replace_value = self.heap_array.pop()
        if len(self.heap_array) > 0:
            self.heap_array[0] = replace_value
            
            # percolate down to restore max heap property.
            self.percolate_down(0)
                
        # return the max value
        return max_value
        
# Program to test the heap class.
h = MaxHeap()
input_list = [ 10, 2, 5, 18, 22 ]
for item in input_list: 
    h.insert(item)
    print('   --> array: %s\n' % h.heap_array)
while len(h.heap_array) > 0: 
    removed_value = h.remove()
    print('   --> removed %d, array: %s\n' % (removed_value, h.heap_array))
print()

output:

insert(10):
   --> array: [10]

insert(2):
   --> array: [10, 2]

insert(5):
   --> array: [10, 2, 5]

insert(18):
   percolate_up() swap: 2 <-> 18
   percolate_up() swap: 10 <-> 18
   --> array: [18, 10, 5, 2]

insert(22):
   percolate_up() swap: 10 <-> 22
   percolate_up() swap: 18 <-> 22
   --> array: [22, 18, 5, 2, 10]

remove():
   percolate_down() swap: 10 <-> 18
   --> removed 22, array: [18, 10, 5, 2]

remove():
   percolate_down() swap: 2 <-> 10
   --> removed 18, array: [10, 2, 5]

remove():
   --> removed 10, array: [5, 2]

remove():
   --> removed 5, array: [2]

remove():
   --> removed 2, array: []

Notice how when we remove items, they are removed in sorted (descending) order

Heap Sort: Main Idea

  1. start with unordered array
  2. push each value onto heap
  3. pop until empty
  4. done!

How do we find the first non leaf node?

[5, 5, 7, 3, 9, 2, 8]
       ^
       first non-leaf node (index = (6//2)-1 = 2)

Heap Sort Code

# Binary max heap percolate down
def max_heap_percolate_down(node_index, heap_list, list_size):
    child_index = 2 * node_index + 1
    value = heap_list[node_index]

    while child_index < list_size:
        # Find the max among the node and all the node's children
        max_value = value
        max_index = -1
        i = 0
        while i < 2 and i + child_index < list_size:
            if heap_list[i + child_index] > max_value:
                max_value = heap_list[i + child_index]
                max_index = i + child_index
            i = i + 1
                                    
        if max_value == value:
            return

        # Swap heap_list[node_index] and heap_list[max_index]
        temp = heap_list[node_index]
        heap_list[node_index] = heap_list[max_index]
        heap_list[max_index] = temp
        
        node_index = max_index
        child_index = 2 * node_index + 1


# Sorts the list of numbers using the heap sort algorithm
def heap_sort(numbers):
    # Heapify numbers list
    i = len(numbers) // 2 - 1
    while i >= 0:
        max_heap_percolate_down(i, numbers, len(numbers))
        i = i - 1
                
    i = len(numbers) - 1
    while i > 0:
        # Swap numbers[0] and numbers[i]
        temp = numbers[0]
        numbers[0] = numbers[i]
        numbers[i] = temp

        max_heap_percolate_down(0, numbers, i)
        i = i - 1

Python heapq module

import heapq

heap = [] # just a normal list

# Insert elements into the heap
for i in [10, 2, 5, 18, 22]:
    heapq.heappush(heap, i)
	
# Heaps in heapq are min heaps!
print(heap) # [2, 10, 5, 18, 22]
while heap: 
    smallest_element = heapq.heappop(heap)

# Using heapify() to convert list into heap
lst = [5, 5, 7, 3, 9, 2, 8]
heapq.heapify(lst)
print(lst) # [2, 3, 5, 5, 9, 7, 8]

2025-11-14

talked about mini-project due 2025-12-10
watched Veritasium video on morse & qr codes

Fixed-length compression codes:

Variable-length compression codes:

Prefix Codes

    start
   /    \
  0      1
 / \    / \
0   1  0   1
^   ^  ^   ^
A   B  C   D

Huffman Codes

 / \
a   b

a=0, b=1

   / \ 
  0   c
 / \
a   b

a=00, b=01, c=1

Huffman Encoding Algorithm:

  abcd:10
 /    \
d:4   abc:6
     /    \ 
   c:3    ab:3
          /   \
         a:1   b:2

(0 is left, 1 is right)
a=110, b=111, c=10, d=0

2025-11-17

Graph Representation

V = {1, 2, 3, 4, 5, 6}
E = {(1,2), (2,3), (3,4), (4,2), (5,3)}

Graph Applications

Graph Properties

  1. Directed vs. Undirected Graphs
    Definition: Directed graphs use arrows to show one-way movement between nodes, while undirected graphs use lines to show two-way, mutual connections.
   Directed (Digraph)      Undirected
   (1) ----> (2)           (1) ----- (2)
    ^         |             |         |
    |         v             |         |
   (3) <---- (4)           (3) ----- (4)
  1. Weighted vs. Unweighted Graphs
    Definition: Weighted graphs assign a numerical cost or value to each edge, whereas unweighted graphs treat every connection as having equal value.
   Weighted                Unweighted
   (1) --5-- (2)           (1) ----- (2)
    |         |             |         |
    3         8             |         |
    |         |             |         |
   (3) --1-- (4)           (3) ----- (4)
  1. Cyclic vs. Acyclic Graphs (Directed)
    Definition: A cyclic graph contains at least one path allowing a return to the start, while an acyclic graph (DAG) progresses strictly forward without loops.
   Cyclic                  Acyclic
   (1) ----> (2)           (1) ----> (2)
    ^         |             |         |
    |         v             v         v
   (3) <---- (4)           (3) ----> (4)
  1. Connected vs. Disconnected Graphs
    Definition: A connected graph has a path between every pair of nodes, while a disconnected graph has isolated nodes or separate islands of nodes.
   Connected               Disconnected
   (1) --- (2)             (1)    (2)---(5)
     \     /                |      |
      \   /                (3)    (4)
       (3)
  1. Simple vs. Non-simple Graphs
    Definition: Simple graphs allow only one edge between unique nodes, whereas non-simple graphs allow multiple edges between the same nodes or self-loops.- non-simple graphs can have self-directed edges and repeated edges
   Simple                  Non-simple
                           (1) === (2)  <-- Multi-edge
   (1) ----- (2)
                           (3)<-- 
                            |    |       <-- Self-loop
                             \__/

Adjacency List Representation:

Example graph:

(0) -------- (1)
 |          / |  \
 |        /   |   \
 |      /     |    (2)
 |    /       |   /
 |  /         |  /
 (4) ------- (3)

for each node, an adjacency list stores a list of its neighbors

graph = {
0: [1,4]
1: [0,2,3,4]
2: [1,3]
3: [1,2,4]
4: [0,1,3]
}

Edge List File Format

5 7 (num_nodes, num_edges) <- optional header, but convenient
0 1
1 2
2 3
3 4
4 0
1 4
1 3 (note: weighted graph would have a third entry for weight)

Creating a graph (adjacency list) from an edge list

from collections import defaultdict

dd = defaultdict(list) # "factory method" - you give it the function to call if you get a keyError
					   # (here, it will create an empty list)

dd[3].append(1) # works!

# Represent graph as adjacency list.
import sys
from collections import defaultdict

# Type declaration
AdjacencyList = dict[int, list[int]]

def read_graph(stream) -> AdjacencyList:
    # Read number of vertices and number of edges
    num_vertices, num_edges = [int(x) for x in stream.readline().split()]

    # Initialize empty adjacency list
    # Use defaultdict to automatically create empty neighbor
    # lists for vertices that have not been encountered yet
    # prior to appending neighbors
    graph = defaultdict(list)

    # Read each edge and update adjacency list
    for _ in range(num_edges):
        source, target = [int(x) for x in stream.readline().split()]

        # Update both directions since graph is undirected
        graph[source].append(target)
        graph[target].append(source)

    return graph

def main(stream=sys.stdin) -> None:
    # read a single graph
    graph = read_graph(stream)

    # print the adjacency list with vertices in sorted order
    for vertex, neighbors in sorted(graph.items()):
        print(f'{vertex}: {sorted(neighbors)}')

if __name__ == '__main__':
    main()

Adjacency Matrix

(for exmaple graph above)
    0 1 2 3 4
  +-----------
0 | 0 1 0 0 1
1 | 1 0 1 1 1
2 | 0 1 0 1 0
3 | 0 1 1 0 1
4 | 1 1 0 1 0

Advantages of Adjacency Matrices:

Adjacency Matrix in Python

graph = [
[0,1,0,0,1],
...
[1,1,0,1,0]
]

python trick - initialize matrix with all zeros using list comprehension:

graph = [[0] * num_vertices for _ in range(num_vertices)]`

2025-11-19

Veritasium video on mouse mazes

Breadth-First Search:

Depth-First Search:

Dealing with Cycles:

Example Graph: Directed w/ Cycles

Edge List:

(source, target)
1 2
1 3
2 3
2 5
3 4
4 5
5 3

Adjacency List (dictionary):

1: [2, 3]
2: [3, 5]
3: [4]
4: [5]
5: [3]

Visualized:

1 ---> 2 -----+
|      |      |
|      v      v
+----> 3 <--- 5
       |      ^
       v      |
       4 -----+

Implementation in Python:

from collections import defaultdict, deque
import sys

# Types

Graph = dict[int, list[int]]

# Functions

def read_graph(stream=sys.stdin) -> Graph:
    graph = defaultdict(list)

    for line in stream:
        source, target = [int(x) for x in line.split()]
        graph[source].append(target)

    return graph

def bfs(graph: Graph, vertex: int) -> None:
    frontier = deque([vertex])   # Vertices to be visited
    visited  = set()             # Vertices already visited

    while frontier:
        vertex = frontier.popleft()

        if vertex in visited:
            continue

        visited.add(vertex)
        
        print(vertex, end=' ')

        for neighbor in graph[vertex]:
            if neighbor not in visited:
                frontier.append(neighbor)
    print()

def dfs(graph: Graph, vertex: int) -> None:
    frontier = deque([vertex])   # Vertices to be visited
    visited  = set()             # Vertices already visited

    while frontier:
        vertex = frontier.pop()

        if vertex in visited:
            continue

        visited.add(vertex)
        
        print(vertex, end=' ')

        for neighbor in graph[vertex]:
            if neighbor not in visited:
                frontier.append(neighbor)
    print()

# Main Execution

def main(stream=sys.stdin):
    graph = read_graph(stream)

    bfs(graph, min(graph.keys()))
    dfs(graph, min(graph.keys()))

if __name__ == '__main__':
    main()

Note how similar BFS and DFS are in this implementation!! - (exactly identical, except bfs pops from left)

2025-11-21

Dijkstra's Algorithm is a Single-Source Shortest Path Algorithm

Algorithm Frontier List Data Structure Visited List Data Structure
DFS Stack Set
BFS Queue Set
Dijkstra's Priority Queue (Min Heap)! Set

Dijkstra's Algorithm is a Greedy Algorithm!!!

two example graphs:

GRAPH 1                                   GRAPH 2                       

A ---4---> B <---1--- D                   A ---4---> B <---1--- D
|          ^          ^                   |                     ^
1          1          1                   1                     1
v          |          |                   v                     |
C ---1---> E -------- +                   C ---1---> E ---1---> F

note how to go from A->B in graph 1 it is fastest to go A->C->E->B, while A->B is fastest in graph 2

Dijkstra's Algorithm pseudocode:

initialize frontier with (0, source node)
while frontier not empty:
    pop vertex with lowest accumulated distance
    if not already visited:
        mark vertex as visited and store distance
        for each neighbor of vertex:
            push (vertex dist + dist to neighbor, neighbor name) to frontier

(note that this is just for finding the length of the shortest distance, we will discuss reconstructing path later.)

2025-11-24

What is the time complexity of Dijkstra's Algorithm?

Dijkstra's Algorithm implemented in Python:

import collections
from heapq import heappush, heappop
import sys

# Types
'''
The graph is represented as an adjacency list using
a dictionary, where the key is the source node and
the value is another dictionary, where the keys
are neigbor vertices and the values are the edge weights
to each vertex, e.g.

{
    source_vertex1 : {neighbor1: weight1, neighbor2: weight2}
    source_vertex2 : . . .
    . . .
}

'''
Graph = dict[str, dict[str, int]]

def read_graph(stream) -> Graph:
    ''' 
    Read in directed graph 
    Each line is an edge: source, target, weight
    '''
    graph = collections.defaultdict(dict)
    for line in stream:
        source, target, weight = line.split()
        graph[source][target] = int(weight)
    return graph

def compute_sssp(graph: Graph, start: str) -> dict[str, int]:
    ''' Use Dijkstra's Algorithm to compute the single-source shortest path '''
    
    # frontier is a priority queue of tuples (distance, vertex)
    frontier: list[tuple[int, str]] = []

    # visited is a dict of vertex:distance
    visited: dict[str, int] = {}

    # use heap to implement frontier priority queue
    heappush(frontier, (0, start))

    while frontier:
        # pop total_distance, vertex from frontier
        total_distance, vertex = heappop(frontier)

        # if vertex in visited, continue to next iteration
        if vertex in visited:
            continue
        
        # add vertex:total_distance to visited
        visited[vertex] = total_distance

        # push each unvisited neighbor with its total_distance to frontier
        for neighbor, weight in graph[vertex].items():
            if neighbor not in visited:
                heappush(frontier, (weight+total_distance, neighbor))

    return visited

# Main Execution

def main(stream=sys.stdin) -> None:
    # Read Graph
    graph   = read_graph(stream)

    # Compute SSSP
    start   = min(graph.keys())
    visited = compute_sssp(graph, start)

    # Display Distances
    for target in sorted(graph.keys())[1:]:
        print(f'{start} -> {target} = {visited[target]}')

if __name__ == '__main__':
    main()

We can now find the length of the shortest path to each node from a given starting node...but how do we find the actual path?

initialize frontier with (0, source node, source node)
while frontier not empty:
    pop vertex with lowest accumulated distance
    if not already visited:
        mark vertex as visited and store distance **and predecessor**!
        for each neighbor of vertex:
            push (vertex dist + dist to neighbor, neighbor name, vertex as predecessor) to frontier

In practice, this means that in our code we would change:

def reconstruct_path(visited: dict[str, tuple[int,str]], origin: str, destination: str) -> list[str]:
    path = []

    # Reconstruct path from destination to origin
    curr = destination
    while curr != origin:
        # Append the current vertex to the end of the path and update the current vertex to its predecessor.
        # Note that the order of the path in the list is reversed, so the path must be reversed before returning.
        path.append(curr)
        curr = visited[curr][1] # predecessor

	print(f"path from {origin} to {destination} is of length {visited[destination][0]}")
    path.append(origin)
    return list(reversed(path))

Next class - Prim's Algorithm!

2025-12-1

Prim's Algorithm

Example graph:

(A)--3--(B)--1--(D)
 |       |       |
 4       5       2
 |       |       |
 +------(C)------+

What is the MST?

How might we implemented this?

Prim's Algorithm Pseudocode

initialize frontier with (0, source node, source node)
while frontier not empty:
    pop vertex with lowest weight
    if not already visited:
        mark vertex as visited and store its predecessor
        for each neighbor of vertex:
            push (weight to neighbor, neighbor name, vertex as predecessor) to frontier

Time Complexity: O(E*logE)

Prim's Algorithm in Python

from collections import defaultdict
from heapq import heappop, heappush
import sys

# Type definition
Graph = dict[str, dict[str, int]]

def read_graph(stream) -> Graph:
    graph: Graph = defaultdict(dict)
    for line in stream:
        source, target, weight = line.split()
        # Graph is undirected, so we add edges in both directions
        graph[source][target] = int(weight)
        graph[target][source] = int(weight)
    return graph

def compute_mst(graph: Graph, origin: str) -> tuple[int, dict[str, str]]:
    '''
    Compute the Minimum Spanning Tree (MST) from the origin vertex.
    Return the total weight of the MST and a dict of {vertex:source, }
    where source is the predecessor of the vertex.
    '''

    # frontier is priority queue of tuples (distance, vertex, source),
    # where source is the predecessor of the current vertex
    frontier = [(0, origin, origin)]

    # visited is a dict of {vertex:source, }
    visited  = {}
    total_weight = 0

    while frontier:
        weight, vertex, source = heappop(frontier)

        if vertex in visited:
            continue

        # add vertex:source to the visited list and update total weight
        visited[vertex] = source
        total_weight += weight

        for neighbor, weight in graph[vertex].items():
            if not neighbor in visited:
                # Push the neighbor to the frontier as a tuple
                # (weight from predecessor, vertex, predecessor)
                heappush(frontier, (weight, neighbor, vertex))

    del visited[origin] # Delete origin vertex from visited list to be returned
    return total_weight, visited

def main(args=None) -> None:
    if args is None:
        args = sys.argv[1:]
    if len(args) != 2:
        print('Usage:  mst_prim.py graph_file origin')
        sys.exit(1)

    with open(args[0], 'r') as stream:
        graph = read_graph(stream)
    
    origin = args[1]

    # MST
    mst_length, mst_edges = compute_mst(graph, origin)
    edges = sorted(sorted(t) for t in mst_edges.items())

    print(f'MST length = {mst_length}')
    print('MST edges: '+' '.join(f'{source}{target}' for source, target in edges))

if __name__ == '__main__':
    main()

Let's recap again:

Algorithm Frontier List Data Structure Visited List Data Structure
DFS Stack Set
BFS Queue Set
Dijkstra's Priority Queue (Min Heap) Set
Prim's Priority Queue (Min Heap) Set
next...

Topological Sort!

A --> B --> E
            ^
			|
C --> D ----+

+-------------------------+
|                         |
v                         |
A -------------> B        |
|                |        |
|                |        |
v                v        |
F        +-----> C <------D
|        |
|        |         
+------> E

some possible orderings:

Degree of a vertex:

<--D--> degree = 0

-->B    degree = 1

   v 
-->C<-- degree = 3

degrees = {
	A: degree,
	...
	E: degree
}

How might we implement an algorithm to find viable topological orderings?

Kahn's Topological Sort Algorithm

create table of degrees for each node
add vertices with degree 0 to frontier
while the frontier not empty:
	pop vertex
	append to visited
	for each neighbor of vertex:
		decrement degree
		if degree equals 0, append to frontier

2025-12-3

Last time we covered topological sort. Question: what happens if a graph has cycles?

Complexity of Kahn's Algorithm:

  1. compute the in-degree for every vertex (E edges total) -> O(E)
  2. we visit each vertex once -> O(V)
  3. for each vertex, we must decrement (and potentially push) nodes along each edge -> O(E)
    Adding up, this gives us O(V + E)

Implementing Kahn's Topological Sort in Python

Example Application: Makefile!! (in what order should we process the files?)

library.o:  	library.c library.h
	$(CC) $(CFLAGS) -o library.o -c library.c

main.o:     	main.c library.h
	$(CC) $(CFLAGS) -o main.o -c main.c

program:    	main.o library.o
	$(CC) $(LDFLAGS) -o program main.o library.o

A makefile is a graph:

main.c       library.h       library.c
   |            |   |             |
   |    +-------+   +-------+     |
   |    |                   |     |
   v    v                   v     v
 (main.o)               (library.o)
    |                       |
    +-----------+-----------+
                |
                v
           [ program ]

from collections import defaultdict
import sys

# Type definition
Graph = dict[str, set[str]]

def read_edgefile(stream) -> Graph:
    graph: Graph = defaultdict(set)

    for line in stream:
        source, target = line.split()
        graph[source].add(target)

    return graph

def read_makefile(stream) -> Graph:
    graph: Graph = defaultdict(set)

    for line in stream:
        if ':' not in line:
            continue

        targets_string, sources_string = line.split(':')
        targets = targets_string.split()
        sources = sources_string.split()

        for source in sources:
            graph[source].update(targets)

    return graph

def compute_degrees(graph: Graph) -> dict[str, int]:
    # degrees is a dictionary {vertex:incoming_edges}
    # defaultdict is used to create a default value of 0
    degrees: dict[str, int] = defaultdict(int)

    for source, targets in graph.items():
        # If the source hasn't been seen yet, include it in the dictionary with a value of 0
        degrees[source]
        # For each target, increment the number of incoming edges
        for target in targets:
            # Creates an entry with value 0 before incrementing
            degrees[target] += 1

    return degrees

def topological_sort(graph: Graph) -> list[str]:
    visited  = []
    degrees  = compute_degrees(graph)

    # Initialize the frontier with vertices that have no incoming edges
    frontier = [node for node,degree in degrees.items() if degree==0]

    while frontier:
        vertex = frontier.pop()
        visited.append(vertex)

        for neighbor in graph[vertex]:
            degrees[neighbor] -= 1
            if degrees[neighbor] == 0:
                frontier.append(neighbor)

    return visited

def main(args=None) -> None:
    if args is None:
        args = sys.argv[1:]

    # Set the name of the function to be called to read the graph depending on whether
    # the first argument is '-m' for a makefile or otherwise for an edgefile
    if args[0] == '-m':
        args = args[1:]
        read_graph = read_makefile
    else:
        read_graph = read_edgefile

    with open(args[0], 'r') as stream:
        graph = read_graph(stream)

    vertices = topological_sort(graph)

    if len(vertices) == len(graph):
        print(' '.join(vertices))
    else:
        print('There is a cycle!')

if __name__ == '__main__':
    main()

2025-12-5

(bonus topics, not on exam)

N Queens

example configuration with N=4 queens:

-------------------------
|     |  Q  |     |     |
| --- | --- | --- | --- |
|     |     |     |  Q  |
| --- | --- | --- | --- |
|  Q  |     |     |     |
| --- | --- | --- | --- |
|     |     |  Q  |     |
-------------------------

Idea:

we don't need to store an entire matrix to represent the board!

Candidate List (iterative backtracking):

How to determine if a spot is safe?

def solve_n_queens(n):
    # candidates: stores valid board configurations for placing `row` queens
    candidates = [[] for _ in range(n + 1)]
    candidates[0] = [[]]  # Base case: one way to place 0 queens

    # Iterate row by row, building configurations
    for row in range(1, n + 1):
        for config in candidates[row - 1]:  # Take each valid configuration from the previous row
            for col in range(n):  # Try placing a queen in each column
                if is_safe(config, row - 1, col):
                    candidates[row].append(config + [col])

    return candidates[n]

def is_safe(board, row, col):
    # Check previous queens for conflicts
    for r, c in enumerate(board):
        if c == col or abs(c - col) == abs(r - row):
            return False
    return True

def print_solutions(n, solutions):
    for solution in solutions:
        for row in solution:
            print(" ".join("Q" if i == row else "." for i in range(n)))
        print("\n")

# Example usage
n = 4
solutions = solve_n_queens(n)
print(f"Found {len(solutions)} solutions for {n}-Queens.")
print_solutions(n, solutions[:1])  # Print the first solution

at-home exercise: implement recursive N-Queens algorithm!

Longest Common Substring (Dynamic Programming)

What is the longest common substring between "BREAK" and "BEAK"?

B R E A K
B 1 0 0 0 0
E 0 0 1 0 0
A 0 0 0 2 0
K 0 0 0 0 3

max element in table: 3 => longest common substring is of length 3 ending with K
small optimization: we don't need to store the whole table, just the previous row
- still O(N*M) time complexity, but now O(M) space complexity

def longest_common_substring_optimized(str1, str2):
    # Create one row of the matrix.
    matrix_row = [0] * len(str2)

    # Variables to remember the largest value, and the row it occurred at.
    max_value = 0
    max_value_row = 0
    for row in range(len(str1)):
        # Variable to hold the upper-left value from the current matrix position.
        up_left = 0
        for col in range(len(str2)):
            # Save the current cell's value; this will be up_left for the next iteration.
            saved_current = matrix_row[col]
        
            # Check if the characters match
            if str1[row] == str2[col]:
                matrix_row[col] = 1 + up_left
                
                # Update the saved maximum value and row, if appropriate.
                if matrix_row[col] > max_value:
                    max_value = matrix_row[col]
                    max_value_row = row
            else:
                matrix_row[col] = 0
                
            # Update the up_left variable
            up_left = saved_current

    # The longest common substring is the substring in str1 
    # from index max_value_row - max_value + 1, 
    # up to and including max_value_row.
    start_index = max_value_row - max_value + 1
    return str1[start_index : max_value_row + 1]

2025-12-8

(no lecture)

2025-12-10

Final Exam Review (Kahoot!)